两平行板间有水平匀强电场，一根长为L，不可伸长的不导电细绳的一端连着一个质量为m、带电量为q的小球，另一端固定于O点．把小球拉起直至细线与电场线平行，然后无初速度释放
◎ 题目
| 两平行板间有水平匀强电场，一根长为L，不可伸长的不导电细绳的一端连着一个质量为 m、带电量为q的小球，另一端固定于O点．把小球拉起直至细线与电场线平行，然后无初速度释放．已知小球摆到最低点的另一侧，线与竖直方向的最大夹角为θ=30°求： （1）匀强电场的场强 （2）小球到最低点的速度 （3）经过最低点时，细线对小球的拉力 （4）小球运动过程中线的最大张力．  |
◎ 答案
| （1）根据动能定理研究小球从释放到最低点到最低点的另一侧的过程列出等式 小球无初速度释放摆到最低点的另一侧的过程： mgLcosθ-qEL（1+sinθ）=0-0=0 θ=30° 解得：E=
（2）根据动能定理研究小球从释放到最低点的过程得： mgL-qEL=
由①②得：v=
（3）小球最低点时由重力和细线的拉力的合力提供小球的向心力， 根据牛顿第二定律得 F-mg=m
由③④得：F=
（4）将电场力与重力合成F合=
在O'点产生最大加速度，对应最大拉力． 由几何关系得 α=60°． 根据动能定理研究O点到O'点，得： mg? |
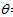
![质量为1500kg的汽车在平直的公路上运动，v-t图象如图所示。由此不可求出的下列物理量是[]A．前25s内汽车的平均速度B．前l0s内汽车的加速度C．前l0s内汽车所受的阻力D．15～25s内合](http://www.00-edu.com/d/file/2022-11-05/6634ddaad6711d5db061211ee3b3344b.gif)
![质量为1500kg的汽车在平直的公路上运动，v-t图象如图所示。由此可求[]A.前25s内汽车的平均速度B.前10s内汽车的加速度C.前10s内汽车所受的阻力D.15～25s内台外力对汽车所做](http://www.00-edu.com/d/file/2022-11-05/2d11ece61cc5126253c6d5ed0aa8059b.gif)
