如图所示,在游乐节目中,要求选手从高为H的平台上A点由静止出发,沿着动摩擦因数为μ的滑道向下运动到B点后水平滑出,最后刚好落到水池中的浮台上.设滑道可以伸缩,其水平距
◎ 题目
如图所示,在游乐节目中,要求选手从高为H的平台上A点由静止出发,沿着动摩擦因数为μ的滑道向下运动到B点后水平滑出,最后刚好落到水池中的浮台上.设滑道可以伸缩,其水平距离为L,B点的高度h可由选手自由调节(取g=10m/s2).要求: (1)选手到达B点的速度表达式; (2)试证明选手落到浮台上的速度大小与B点的高度h无关; (3)同学甲认为B点的高度h越大,选手在空中飞越的时间越长,在浮台上的落点距岸边C越远;同学乙认为B点的高度h越小,选手到达B点的水平速度越大,在浮台上的落点距岸边C越远,请通过推算说明你的观点. |
◎ 答案
| (1)由A运动到B过程,设滑道倾角为θ, 则由牛顿第二定律得:mgsinθ-μmgcosθ=ma 又:vB2-0=
且:tanθ=
解得:vB=
(2)平抛运动过程: 竖直方向:vy2=2gh 水平方向:vx2=vB2=2g(H-h-μL) 选手落到浮台上的速度大小:v=
(3)设选手在浮台上的落点距岸边C的距离为S, 对平抛运动过程:S=vBt h=
得:S=
|


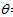
![质量为1500kg的汽车在平直的公路上运动,v-t图象如图所示。由此不可求出的下列物理量是[]A.前25s内汽车的平均速度B.前l0s内汽车的加速度C.前l0s内汽车所受的阻力D.15~25s内合](http://www.00-edu.com/d/file/2022-11-05/6634ddaad6711d5db061211ee3b3344b.gif)
![质量为1500kg的汽车在平直的公路上运动,v-t图象如图所示。由此可求[]A.前25s内汽车的平均速度B.前10s内汽车的加速度C.前10s内汽车所受的阻力D.15~25s内台外力对汽车所做](http://www.00-edu.com/d/file/2022-11-05/2d11ece61cc5126253c6d5ed0aa8059b.gif)
