一探险队在探险时遇到一山沟,山沟的一侧OA竖直,另一侧的坡面OB呈抛物线形状,与一平台BC相连,如图所示.已知山沟竖直一侧OA的高度为2h,平台离沟底h高处,C点离竖直OA的水
◎ 题目
| 一探险队在探险时遇到一山沟,山沟的一侧OA竖直,另一侧的坡面OB呈抛物线形状,与一平台BC相连,如图所示.已知山沟竖直一侧OA的高度为2h,平台离沟底h高处,C点离竖直OA的水平距离为2h.以沟底的O点为原点建立坐标系xOy,坡面的抛物线方程为y=x2/2h.质量为m的探险队员从山沟的竖直一侧,沿水平方向跳向平台.人视为质点,忽略空气阻力,重力加速度为g.求: (1)若探险队员以速度v0水平跳出时,掉在坡面OB的某处,则他在空中运动的时间为多少? (2)为了能跳在平台上,他的初速度应满足什么条件?请计算说明. (3)若已知探险队员水平跳出,刚到达OBC面的动能Ek=1.55mgh,则他跳出时的水平速度可能为多大? 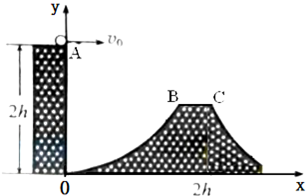 |
◎ 答案
| (1)设探险队员跳到坡面上时水平位移为x,竖直位移为H, 由平抛运动规律有: x=v0t ① H=
根据几何关系有: y=2h-H 由于落在OB上满足抛物体线方程即 y=
2h-H=
由①②③可解得H=
即运动时间t=
(2)若探险员掉在C处,根据题意应该满足几何关系有: ∵h=
∴t=
又∵x=2h=v0t ∴v0=
若探险员掉在B 处,有: h=
x= |






