如图所示,光滑水平面上,质量为2m的小球B连接着轻质弹簧,处于静止;质量为m的小球A以初速度v0向右匀速运动,接着逐渐压缩弹簧并使B运动,过一段时间,A与弹簧分离.(弹簧始
◎ 题目
| 如图所示,光滑水平面上,质量为2m的小球B连接着轻质弹簧,处于静止;质量为m的小球A以初速度v0向右匀速运动,接着逐渐压缩弹簧并使B运动,过一段时间,A与弹簧分离.(弹簧始终处于弹性限度以内) (1)在上述过程中,弹簧的最大弹性势能是多大; (2)若开始时在B球的右侧某位置固定一块挡板(图中未画出),在A 球与弹簧分离之前使B球与挡板发生碰撞,并在碰后立刻将挡板撤走.设B球与固定挡板的碰撞时间极短,碰后B球的速度大小不变但方向相反.试求出此后弹簧的弹性势能最大值的范围. 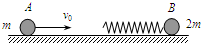 |
◎ 答案
| (1)当A球与弹簧接触以后,在弹力作用下减速运动,而B球在弹力作用下加速运动,弹簧势能增加,当A、B速度相同时,弹簧的势能最大. 设A、B的共同速度为v,弹簧的最大势能为E,则A、B系统动量守恒:mv0=(m+2m)v① 由机械能守恒:
联立两式得:E=
(2)设B球与挡板碰撞前瞬间的速度为vB,此时A的速度为vA. 系统动量守恒:mv0=mvA+2mvB…④ B与挡板碰后,以vB向左运动,压缩弹簧,当A、B速度相同(设为v共)时,弹簧势能最大,为Em,则:mvA-2mvB=3mv共…⑤
由④⑤两式得:v共=
而当弹簧恢复原长时相碰,vB有最大值vBm,则: mv0=mvA′+2mvBm
联立以上两式得:vBm=
上一篇:如图甲所示,一轻弹簧的两端与质量分别为m1和m2的两物块A、B相连接,并静止在光滑的水平面上,已知两物体的质量之比为m1:m2=1:2,现使A瞬时获得水平向右的速度3m/s,以此刻为
下一篇:如图所示,离水平地面高1.5L的一个光滑小定滑轮上,静止地搭着一根链条.该链条长为L,质量为m(可以看作质量分布均匀).由于受到一个小小的扰动,链条开始无初速滑动,最后落
零零教育社区:论坛热帖子
|






