如图所示,在光滑水平轨道上有一小车质量为2m,它下面用长为L的绳系一质量也为2m的小砂袋,系统原来处于静止.今有以水平速度V0水平射来的质量为m的子弹,它射入砂袋后并不穿
◎ 题目
| 如图所示,在光滑水平轨道上有一小车质量为2m,它下面用长为L的绳系一质量也为2m的小砂袋,系统原来处于静止.今有以水平速度V0水平射来的质量为m的子弹,它射入砂袋后并不穿出(射入时间极短)而与砂袋一起摆动.不计悬线质量,试求: (1)子弹射入砂袋过程的发热量Q (2)子弹和砂袋能达到的最大高度h. 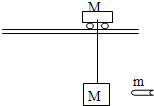 |
◎ 答案
| (1)子弹射入砂袋过程中的发热量等于子弹和砂袋组成的系统损失的机械能 又子弹射入砂袋的过程中,系统在水平方向动量守恒有: m子v0=(m子+m砂)v1 得v1=
∴Q=
(2)根据题意知子弹和砂袋一起摆到最大高度时,砂袋和子弹在竖直方向速度刚好为0,在水平方向速度与小车速度相同,故: 根据动量守恒有(m子+m砂)v1=(m子+m砂+m车)v2 代入数据得系统在水平方向共同速度v2=
又在砂袋和子弹上摆的过程中,系统的机械能守恒:砂袋和子弹增加的势能等于系统减少的动能 所以:g(m子+m砂)hmax=
得:hmax=
答:子弹射入砂袋过程的发热量Q=
|






