如图所示,光滑内壁的半球形碗,半径为R固定在水平桌面上,质量分别为M、m可视为质点的A、B两球,用轻绳相连(不可伸缩),A由碗沿从静止释放①小球A能到达碗底,M与m的关系满足
◎ 题目
| 如图所示,光滑内壁的半球形碗,半径为R固定在水平桌面上,质量分别为M、m可视为质点的A、B两球,用轻绳相连(不可伸缩),A由碗沿从静止释放 ①小球A能到达碗底,M与m的关系满足什么条件? 当M=2m时,②A球到达最高点时A与圆心连线与水平方向的夹角θ为多少? ③A到达碗底时,A、B球速度. 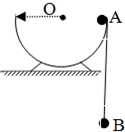 |
◎ 答案
| (1)小球A能到达碗底,则到达碗底的速度v≥0,根据机械能守恒定律得: MgR-mg
解得:M≥
(2)当M=2m时,A球到达最高点时A的速度为vA=0,则vB=0,设B上升的高度为l,则有: 2mglsinθ=mgl 解得:sinθ=
所以θ=30° (3)由于AB为连接体,A到达碗底时有:vA=vBcos45°=
AB系统机械能守恒,则有: 2mgR-mg
解得:vA=
|






