光滑曲面轨道末端切线水平,轨道末端点距离水平地面的高度为H=0.8m,一长度合适的木板两端分别搁在轨道末端点和水平地面之间,构成倾角为θ=37°的斜面,如图所示.一可视为质
◎ 题目
| 光滑曲面轨道末端切线水平,轨道末端点距离水平地面的高度为H=0.8m,一长度合适的木板两端分别搁在轨道末端点和水平地面之间,构成倾角为θ=37°的斜面,如图所示.一可视为质点的质量m=1kg小球,从距离轨道末端竖直高度为h=0.2m处由静止滑下.(不计空气阻力,取g=10m/s2,sin37°=0.6,cos37°=0.8) (1)求小球从轨道末端点冲出瞬间的速度v0的大小; (2)求小球从轨道末端点冲出后,第一次撞击木板时的位置距离木板上端点多远; (3)若改变木板的长度,并使木板两端始终与平台和水平面相接,试通过计算推导小球第一次撞击木板时的动能随木板倾角θ的关系式,并在图中作出Ek-(tanθ)2图象. 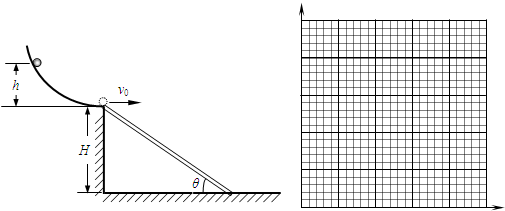 |
◎ 答案
(1)小球下滑过程中机械能守恒,所以有:mgh=
故小球从轨道末端点冲出瞬间的速度v0=2m/s. (2)当小球撞到木板上时,其位移与水平方向夹角为θ,则有:tanθ =
水平方向:x=v0t ② 竖直方向:y=
平抛位移:s=
联立①②③④解得:s=0.75m. 故第一次撞击木板时的位置距离木板上端点距离为0.75m. (3)当小球撞击木板时有:tanθ =
所以:vy=gt=2v0tanθ 所以:Ek=
|






