如图所示,A、B两小球大小相同,A绝缘且不带电,B带正电,其质量之比为1:3,现让A球从光滑绝缘的四分之一圆弧轨道的项点由静止释放,当与静止在轨道最低点的B球发生完全弹性
◎ 题目
| 如图所示,A、B两小球大小相同,A绝 缘且不带电,B带正电,其质量之比为1:3,现让A 球从光滑绝缘的四分之一圆弧轨道的项点由静止 释放,当与静止在轨道最低点的B球发生完全弹性 碰撞后,B球飞入右边的匀强电场区.场强方向水平向左,最终B球恰好落至离抛出点的正下方h处的 C点,已知圆弧轨道半径为R,重力加速度为g. 求:(1)碰撞后,A球离C点的最大竖直高度; (2)B球的最大水平位移; (3)B球受到的电场力F与重力G的大小之比. 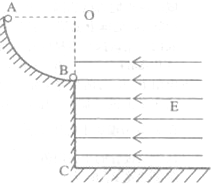 |
◎ 答案
| (1)设A球与B球碰撞前的速度为VA,碰撞后的A、B的速度分别为VA′和VB′,则: 由动能定理得:
由动量守恒得:mAVA=mAVA′+mBVB′② A球与B球发生完全弹性碰撞机械能守恒,
A、B质量之比为1:3,④ 联立以上式子解得: VA′=-
即A球反向运动. 设A上升到离圆弧轨道最低点的最大高度为H,由机械能守恒:
解得:H=
所以A球离C点的最大高度为h+
(2)B球的运动轨迹如图中虚线,其运动分为两个运动: 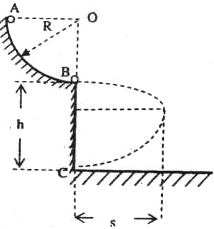 即:水平方向匀减速直线运动和竖直方向的自由落体运动,设B球运动时间为2t, 最大水平位移为S,由于两个分运动的等时性和水平方向的对称性得:
解得:S=
(3)设电场力产生的加速度为a,S= |






