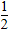某同学想利用古代抛石机的模型验证系统机械能守恒定律,如图1所示,一轻杆可绕固定于水平地面的竖直支架上的转动轴O转动,轻杆左端固定一小球A,轻杆右端的勺形槽内放置另一
◎ 题目
| 某同学想利用古代抛石机的模型验证系统机 械能守恒定律,如图1所示,一轻杆可绕固定于水平地面的竖直支架上的转动轴O转动,轻杆左端固定一小球A,轻杆右端的勺形槽内放置另一小球B.当将轻杆由静止释放后,A球向下运动可带动轻杆逆时针转动,直到轻杆到达竖直位置时,B球被水平抛出.实验前已测得小球A、B的质量分别为mA、mB,A、B的球心离O的距离分别为LA、LB,转轴O离地面的高度为h0,已知重力加速度为g. (1)该同学在某次实验时,将轻杆从水平位置无初速释放,则从释放到B球刚被抛出的过程中,系统势能的减少量为______;B球落地后,测得B球落地点与O点的水平距离为s,则由此可知,从释放到B球刚被抛出的过程中,系统动能的增加量为______. (2)(多选题)为减小实验误差,可采取的措施有______ (A)尽量减小B球的质量 (B)选用硬度较高的轻杆 (C)尽量减小转轴O处的摩擦 (D)在同一高度多次释放A球的前提下,取B球的平均落点,然后测量s (3)为进一步提高实验精度,也可多次改变A球释放的初始位置,如图2所示.测出A球离地高度h及对应的B球落地点与O点的水平距离s,然后根据测量数据作______图象,若得到一条过原点的直线,也可证明系统机械能守恒. 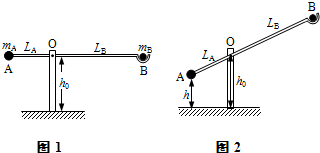 |
◎ 答案
| (1)由题意可知,小球A下降,B球上升,则重力势能的差值,转化为两小球的动能,由于小球B在最高点做平抛运动,所以根据水平位移s,竖直高度h0+LB, 从而求出抛出速度为v=
(2)为减小实验误差,杆必须有硬度,否则会储存弹性势能,同时转轴尽量减小摩擦阻力,最后要确定B球的落点,因此多次释放,取平均值. 故选BCD. (3)为进一步提高实验精度,也可多次改变A球释放的初始位置,测出A球离地高度h及对应的B球落地点与O点的水平距离s, 当根据数据作出((LA-h0+h)---s2),因为在改变h时,抛出水平距离也会发生变化,所以作出此图象若是过原点,则能验证机械能守恒. 故答案为:(1)mAgLA-mBgLB;
|
◎ 解析
“略”◎ 知识点
- 最新内容
- 相关内容
- 网友推荐
- 图文推荐
上一篇:(1)有一游标卡尺,主尺的最小分度是1mm,游标上有20个小的等分刻度.用它测量一小球的直径,如图甲所示的读数是______mm.用螺旋测微器测量一根金属丝的直径,如图乙所示的读数
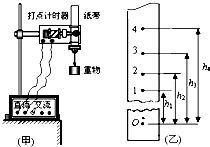
下一篇:某同学利用如图甲所示的实验装置验证机械能守恒定律.该同学经正确操作得到打点纸带,在纸带后段每两个计时间隔取一个计数点,依次为1、2、3、4、5、6、7,测量各计数点到第一
零零教育社区:论坛热帖子
| [高考] 2022 西安电子科技大学《软件工程》大作业答案 (2022-04-25) |
| [家长教育] 孩子为什么会和父母感情疏离? (2019-07-14) |
| [教师分享] 给远方姐姐的一封信 (2018-11-07) |
| [教师分享] 伸缩门 (2018-11-07) |
| [教师分享] 回家乡 (2018-11-07) |
| [教师分享] 是风味也是人间 (2018-11-07) |
| [教师分享] 一句格言的启示 (2018-11-07) |
| [教师分享] 无规矩不成方圆 (2018-11-07) |
| [教师分享] 第十届全国教育名家论坛有感(二) (2018-11-07) |
| [教师分享] 贪玩的小狗 (2018-11-07) |