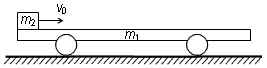
如图所示,A、B是静止在水平地面上完全相同的两块长木板.A的左端和B的右端相接触.两板的质量皆为M=2.0kg,长度皆为l=1.0m.C是一质量为m=1.0kg的小物块.现给它一初速度v0=
◎ 题目
如图所示,A、B是静止在水平地面上完全相同的两块长木板.A的左端和B的右端相接触.两板的质量皆为M=2.0kg,长度皆为l=1.0m.C是一质量为m=1.0kg的小物块.现给它一初速度v0=2.0m/s,使它从B板的左端开始向右滑动.已知地面是光滑的,而C与A、B之间的动摩擦因数皆为μ=0.10.求最后A、B、C各以多大的速度做匀速运动.取重力加速度g=10m/s2. |
◎ 答案
| 先假设小物块C在木板B上移动x距离后,停在B上.这时A、B、C三者的速度相等,设为v,由动量守恒得: mv0=(m+2M)v ① 在此过程中,木板B的位移为s,小木块C的位移为s+x,由功能关系得: 对C有:-μmg(s+x)=
此时AB是个整体有:μmgs=
②③相加得:-μmgx=
解①、④两式得: x=
代入数值得:x=1.6m x比B板的长度l大,这说明小物块C不会停在B板上,而要滑到A板上.设C刚滑到A板上的速度为v1,此时A、B板的速度为V1,则由动量守恒得: mv0=mv1+2MV1 ⑤ 由功能关系得:
联立⑤⑥带入数据得:V1=
|