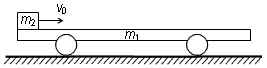
如图所示,高为H=0.45m的台面上有轻质细绳,绳的一端系一质量为m=0.1kg的小球P,另一端挂在光滑的水平轴上O上,O到小球P的距离为R=0.1m,小球与台面接触,但无相互作用,
◎ 题目
| 如图所示,高为H=0.45m的台面上有轻质细绳,绳的一端系一质量为m=0.1kg的小球P,另一端挂在光滑的水平轴上O上,O到小球P的距离为R=0.1m,小球与台面接触,但无相互作用,在小球两侧等距离各为L=0.5m处,分别固定一光滑斜面及一水平向左运动的传送带,传送带长为d=0.9m,运行速度大小为v=3m/s,现有一质量也为m可视为质点的小滑块Q从斜面上的A处无初速滑下(A距台面高h=0.7m),至C处与小球发生弹性碰撞,已知滑块与台面的动摩擦因数为μ1=0.5,与传送带之间动摩擦因数为μ2=0.25,不计传送带高度,及滑轮大小对问题的影响.(重力加速度g=10m/s2) 求: (1)当小球被撞后做圆周运动到最高点时对轻绳的作用力大小? (2)滑块的最终位置与传送带末端的E的距离? (3)整个过程传送带电机消耗的电能?  |
◎ 答案
| (1)对滑块Q从A到C根据动能定理有: mgh-μ1mgl=
PQ发生弹性碰撞,因质量相等,故交换速度,撞后P的速度为vc′=vc=3m/s P运动至最高点的速度为vF,根据机械能守恒定律有:
得vF=
P在最高点根据牛顿第二定律有:F+mg=
得F=
根据牛顿第三定律知轻绳受力大小F′=F=4N (2)PQ再撞后再次交换速度对物块有vc″=vc′=3m/s 对物块从C到D根据动能定理有:-μ1mgl=
vD= |