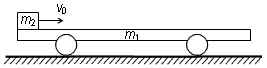
物块A与竖直轻弹簧相连,放在水平地面上,一个物块B由距弹簧上端O点H高处自由落下,落到弹簧上端后将弹簧压缩.为了研究物块B下落的速度随时间变化的规律和物块A对地面的压力
◎ 题目
| 物块A与竖直轻弹簧相连,放在水平地面上,一个物块B由距弹簧上端O点H高处自由落下,落到弹簧上端后将弹簧压缩.为了研究物块B下落的速度随时间变化的规律和物块A对地面的压力随时间变化的规律,某位同学在物块A的正下方放置一个压力传感器,测量物块A对地面的压力,在物块B的正上方放置一个速度传感器,测量物块B下落的速度.在实验中测得:物块A对地面的最小压力为P1,当物块B有最大速度时,物块A对地面的压力为P2.已知弹簧的劲度系数为k,物块B的最大速度为v,重力加速度为g,不计弹簧的质量. (1)物块A的质量. (2)物块B在压缩弹簧开始直到B达到最大速度的过程中,它对弹簧做的功. (3)若用T表示物块B的速度由v减到零所用的时间,用P3表示物块A对地面的最大压力,试推测:物块的速度由v减到零的过程中,物块A对地面的压力P随时间t变化的规律可能是下列函数中的______(要求说明推测的依据) A.P=P2+(P3-P2)
C.P=P2+(P3-P2)
 |
◎ 答案
| (1)物块B没有落到弹簧上时,物块A对地面的压力为最小压力,设此时物块A受重力为mAg,物块受mAg和地面的支持力处于平衡,故:P1=mAg 所以物块A的质量:mA=
(2)物块B落到弹簧上,将弹簧压缩,当物块B的重力等于弹簧的弹力,物块B有最大速度.设物块B的质量为mBg,有最大速度时弹簧压缩量为x1,则: kx1=mBg②即弹簧产生的弹力为mBg 此时,由物块A受弹簧的压力、重力和地面的支持力处于平衡,则有:P2=mAg+mBg③ 物块B由静止开始落下,到达最大速度的过程中,重力做功mBg(H+x1),设克服弹簧的弹力做功W,根据动能定理,有:
将①②③式代人④式,得物块B对弹簧做功W=(P2-P1)(H-
(3)应为C 物块B与弹簧接触后,在重力和弹力作用下,在竖直方向上做简谐运动,周期为4T.物块A对地面的压力大小P等于A的重力与弹簧的弹力之和.则P随时间变化的关系只可是正弦函数,AB选项都不正确.当t=0时,压P=P2;当t=T时,压力最大为P3.只有选项C正确. 另物块B与弹簧接触后,在重力和弹力作用下,在竖直方向上做简谐运动.其平衡位置在物块B具有最大速度处,设平衡位置为0′,建立O′x坐标系,以竖直向下为正方向,有 mBg-F弹=-kx⑤ 物块B做简谐运动的周期为4T,在速度由最大变到零的四分之一周期内,设最大位移为xm,振动位移为 x=xmsin(
 物块A对地面的压力为P=mAg+mBg+kxmsin(
代人③式得P=P2+(P3-P2)
当t=T时,压力最大为P3,即P3=P2+kxmsin(
压力P随时间t变化的规律为P=P2+(P3-P2)
答:(1)A的质量为 |