(22分)整个装置图如图所示,在光滑绝缘水平面上固定一竖直的表面光滑的挡板,ABCD为挡板与水平面的交线,其中ABC为直线,CD为半径R=4.0m的圆弧,C点为AC直线与CD圆弧的切点
◎ 题目
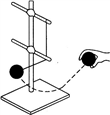
 (22分)整个装置图如图所示,在光滑绝缘水平面上固定一竖直的表面光滑的挡板,ABCD为挡板与水平面的交线,其中ABC为直线,CD为半径R=4.0 m的圆弧,C点为AC直线与CD圆弧的切点。整个装置置于真空中两有界的与水平面平行的匀强电场中,MN为两电场的分界面与水平面的交线,且MN垂直于AB,在MN的左侧有一沿AB方向场强大小为E1=5.0×105 V/m的匀强电场,在MN的右侧有一沿MN方向场强大小为E2=1.0×107 V/m的匀强电场。质量m2=4.0×10-2 kg的不带电金属小球静置于C点,电量为q=+2.0×10-6 C、质量为m1=1.0×10-2 kg的小球Q自A点静止释放(P、Q两金属球的大小完全相同)。已知AB=0.5 m,BC=1.20 m,cos10°=0.985,=π,简谐振动的周期公式为T=2π,式中m为振子的质量,k是回复力与位移大小的比值且为常数。试求P、Q两球在距A点多远处第二次相碰(不计碰撞时机械能损失和电荷间的相互作用力,结果取三位有效数字)。 (22分)整个装置图如图所示,在光滑绝缘水平面上固定一竖直的表面光滑的挡板,ABCD为挡板与水平面的交线,其中ABC为直线,CD为半径R=4.0 m的圆弧,C点为AC直线与CD圆弧的切点。整个装置置于真空中两有界的与水平面平行的匀强电场中,MN为两电场的分界面与水平面的交线,且MN垂直于AB,在MN的左侧有一沿AB方向场强大小为E1=5.0×105 V/m的匀强电场,在MN的右侧有一沿MN方向场强大小为E2=1.0×107 V/m的匀强电场。质量m2=4.0×10-2 kg的不带电金属小球静置于C点,电量为q=+2.0×10-6 C、质量为m1=1.0×10-2 kg的小球Q自A点静止释放(P、Q两金属球的大小完全相同)。已知AB=0.5 m,BC=1.20 m,cos10°=0.985,=π,简谐振动的周期公式为T=2π,式中m为振子的质量,k是回复力与位移大小的比值且为常数。试求P、Q两球在距A点多远处第二次相碰(不计碰撞时机械能损失和电荷间的相互作用力,结果取三位有效数字)。        |
◎ 答案
(22分)解:小球Q由静止开始做匀加速直线运动,设到达B处时速度为v0  则:qE1=m1v 则:qE1=m1v ∴v0===10 m/s (2分) ∴v0===10 m/s (2分) Q球进入电场E2后做匀速运动,与静止在C点的P球发生弹性碰撞,碰后P、Q两球电量等量分配且由动量守恒 Q球进入电场E2后做匀速运动,与静止在C点的P球发生弹性碰撞,碰后P、Q两球电量等量分配且由动量守恒 m1v0=m1v1+m2v2 ① (3分) m1v0=m1v1+m2v2 ① (3分) 又:m1v=m1v+m2v ② (3分) 又:m1v=m1v+m2v ② (3分) 解①、②可得:v1=v0=×10=-6 m/s 解①、②可得:v1=v0=×10=-6 m/s v2==×10=4 m/s (2分) v2==×10=4 m/s (2分) 即碰后Q球返回,先沿CB匀速运动进入E1电场中,开始做匀减速直线运动,速度为零后又反向加速,运动到B以v1=6 m/s从B点再次进入电场E2,由C到B过程中,运动时间: 即碰后Q球返回,先沿CB匀速运动进入E1电场中,开始做匀减速直线运动,速度为零后又反向加速,运动到B以v1=6 m/s从B点再次进入电场E2,由C到B过程中,运动时间: t1==s=0.2 s t1==s=0.2 s 在E1中运动时间为t2,则:t2=,a= 在E1中运动时间为t2,则:t2=,a= ∴t2===0.24 s (2分) ∴t2===0.24 s (2分) P球被碰后沿CD弧运动,设运动到D点且和圆心O的连线与OP夹角为θ,据动能定理: P球被碰后沿CD弧运动,设运动到D点且和圆心O的连线与OP夹角为θ,据动能定理: m2v=qE2R(1-cosθ) m2v=qE2R(1-cosθ) ∴cosθ=1-=0.992>0.985 θ<10° (2分) ∴cosθ=1-=0.992>0.985 θ<10° (2分) 小球在圆弧上运动的过程中,竖直方向上受力平衡,水平方向上受力如图,电场力沿圆弧切线方向的分力为: 小球在圆弧上运动的过程中,竖直方向上受力平衡,水平方向上受力如图,电场力沿圆弧切线方向的分力为:   F=qE2sinθ 此力为使小球P振动的回复力 (1分) F=qE2sinθ 此力为使小球P振动的回复力 (1分) Θθ<10° ∴sinθ≈θ≈ (1分) Θθ<10° ∴sinθ≈θ≈ (1分)    ∴F=qE2x ∴F=qE2x ∴k= x为小球P偏离平衡位置的位移,负号表示回复力F与x的方向相反 (1分) ∴k= x为小球P偏离平衡位置的位移,负号表示回复力F与x的方向相反 (1分) 故P球做简谐振动,其周期为: 故P球做简谐振动,其周期为: T=2π=2π=0.8 s (2分) T=2π=2π=0.8 s (2分) P P
上一篇:伽利略斜面理想实验使人们认识到引入能量概念的重要性。在此理想实验中,能说明能量在小球运动过程中不变的理由是[]A.小球滚下斜面时,高度降低,速度增大B.小球滚上斜面时
下一篇:一小球用轻绳悬挂在某固定点.现将轻绳水平拉直,然后由静止开始释放小球.小球由静止开始运动到最低位置的过程中()A.小球在水平方向的速度逐渐增大B.小球在竖直方向的速度逐
零零教育社区:论坛热帖子
|