如图所示,光滑水平面上,质量为m的小球B连接着轻质弹簧,处于静止状态,质量为2m的小球A以大小为v0的初速度向右运动,接着逐渐压缩弹簧并使B运动,过一段时间,A与弹簧分离
◎ 题目
| 如图所示,光滑水平面上,质量为m的小球B连接着轻质弹簧,处于静止状态,质量为2m的小球A以大小为v0的初速度向右运动,接着逐渐压缩弹簧并使B运动,过一段时间,A与弹簧分离. (1)当弹簧被压缩到最短时,弹簧的弹性势能Ep多大? (2)若开始时在B球的右侧,某位置固定一挡板,在A球与弹簧未分离前使B球与挡板碰撞,并在碰后立刻将挡板撤走,设B球与挡板的碰撞时间极短,碰后B球的速度大小不变但方向相反,欲使此后弹簧被压缩到最短时,弹性势能达到第(1)问中Ep的2.5倍,必须使B球的速度多大时与挡板发生碰撞? 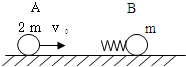 |
◎ 答案
| (1)当弹簧压缩到最短时,A、B的速度相等,2mv0=3mv1 ① A和B的共同速度v1=
根据系统的机械能守恒得
解得 此时弹簧的弹性势能Ep=
(2)B碰挡板时没有机械能损失,碰后弹簧被压缩到最短时,A、B速度也相等,
Ep′=2.5Ep=
解得v2=±
取向右为正方向.若v2=
2mv0=2 mvA+mvB⑥ B球与板碰撞后B与A动量也守恒 2mvA-mvB=3m?
解得 vA=
因为此时vA>vB,弹簧还将继续缩短,所以这种状态是能够出现的, 若v2=-
2mvA-mvB=3mv2=-3m?
由⑥⑧可得,vA=
|






