一轻质弹簧，两端连接两滑块A和B，已知mA=0.99kg，mB=3kg，放在光滑水平桌面上，开始时弹簧处于原长．现滑块A被水平飞来的质量为mC=10g，速度为400m/s的子弹击中，且没有穿出
◎ 题目
| 一轻质弹簧，两端连接两滑块A和B，已知mA=0.99kg，mB=3kg，放在光滑水平桌面上，开始时弹簧处于原长．现滑块A被水平飞来的质量为mC=10g，速度为400m/s的子弹击中，且没有穿出，如图所示，试求： （1）子弹击中A的瞬间A和B的速度 （2）以后运动过程中弹簧的最大弹性势能 （3）B可获得的最大动能．  |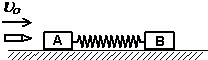
◎ 答案
| （1）子弹击中滑块A的过程，子弹与滑块A组成的系统动量守恒有： mCv0=（mC+mA）vA vA=
子弹与A作用过程时间极短，B没有参与，速度仍为零，故：vb=0． 故子弹击中A的瞬间A和B的速度分别为：vA=4m/s，vb=0． （2）对子弹、滑块A、B和弹簧组成的系统，A、B速度相等时弹性势能最大． 根据动量守恒定律和功能关系可得： mCv0=（mC+mA+mB）v 由此解得：v=
根据功能关系可得： EP=
故弹簧的最大弹性势能为6J． （3）设B动能最大时的速度为vB′，A的速度为vA′，则 （mC+mA）vA=（mC+mA）vA′+mBvB′ 当弹簧恢复原长时，B的动能最大，根据功能关系有：
解得：
B获得的最大动能：
上一篇：下面是一个物理演示实验，它显示：图中自由下落的物体A和B经反弹后，B能上升到比初始位置高得多的地方．A是某种材料做成的实心球，质量m1=0.28kg，在其顶部的凹坑中插着质量m
下一篇：已知氘核质量为2.0136u，中子质量为1.0087u，32He核的质量为3.0150u，（1u相当于931.5MeV的能量）（1）写出两个氘核聚变成32He的核反应方程．（2）计算上述核反应中释放的核能．
零零教育社区：论坛热帖子
|
