(1)如图1,在光滑水平长直轨道上,放着一个静止的弹簧振子,它由一轻弹簧两端各连接一个小球构成,两小球质量相等.现突然给左端小球一个向右的速度u0,求弹簧第一次恢复到自
◎ 题目
| (1)如图1,在光滑水平长直轨道上,放着一个静止的弹簧振子,它由一轻弹簧两端各连接一个小球构成,两小球质量相等.现突然给左端小球一个向右的速度u0,求弹簧第一次恢复到自然长度时,每个小球的速度. (2)如图2,将N个这样的振子放在该轨道上,最左边的振子1被压缩至弹簧为某一长度后锁定,静止在适当位置上,这时它的弹性势能为E0.其余各振子间都有一定的距离,现解除对振子1的锁定,任其自由运动,当它第一次恢复到自然长度时,刚好与振子2碰撞,此后,继续发生一系列碰撞,每个振子被碰后刚好都是在弹簧第一次恢复到自然长度时与下一个振子相碰.求所有可能的碰撞都发生后,每个振子弹性势能的最大值.已知本题中两球发生碰撞时,速度交换,即一球碰后的速度等于另一球碰前的速度. 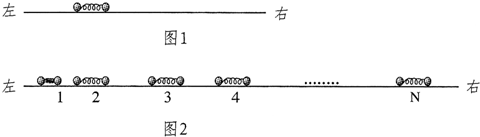 |
◎ 答案
| (1)设每个小球质量为m,以u1、u2分别表示弹簧恢复到自然长度时左右两端小球的速度. 由动量守恒和能量守恒定律有 mu1+mu2=mu0(以向右为速度正方向)
解得u1=u0,u2=0或u1=0,u2=u0 由于振子从初始状态到弹簧恢复到自然长度的过程中,弹簧一直是压缩状态,弹性力使左端小球持续减速,使右端小球持续加速,因此应该取u1=0,u2=u0 即弹簧第一次恢复到自然长度时,左侧小球速度为0,右侧小球速度为u0. (2)以v1、v1′分别表示振子1解除锁定后弹簧恢复到自然长度时左右两小球的速度,规定向右为速度的正方向, 由动量守恒和能量守恒定律, mv1+mv1′=0
解得 v1=
|






