如图所示,质量为m的绝缘球与质量为M=19m的金属球并排悬挂,已知悬挂绝缘球的细线的长度为l.现将绝缘球拉至与竖直方向成θ=600的位置自由释放,下摆后在最低点与金属球发生弹
◎ 题目
| 如图所示,质量为m的绝缘球与质量为M=19m的金属球并排悬挂,已知悬挂绝缘球的细线的长度为l.现将绝缘球拉至与竖直方向成θ=600的位置自由释放,下摆后在最低点与金属球发生弹性碰撞.在平衡位置附近存在垂直于纸面的磁场.已知由于磁场的阻尼作用,金属球将于再次碰撞前停在最低点处.求 (1)绝缘球与金属球第一次碰撞前瞬间的速度大小; (2)绝缘球与金属球第一次碰撞后瞬间的速度大小和方向; (3)经过几次碰撞后绝缘球偏离竖直方向的最大角度将小于450. 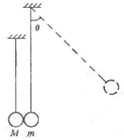 |
◎ 答案
| (1)设小球m的摆线长度为l,小球m在下落过程中与M相碰之前满足机械能守恒: mgl(1-cosθ)=
解得:v0=
(2)m和M碰撞过程满足: mv0=MVM+mv1;
联立得:v1=
(3)由(1)可知,小球m反弹后又以反弹速度v1和小球M发生碰撞,满足: mv1=MVM1+mv2
解得:v2=
整理得:v2=-(
所以:
上一篇:如图,ABD为竖直平面内的光滑绝缘轨道,其中AB段是水平的,BD段为半径R=0.2m的半圆,两段轨道相切于B点,整个轨道处在竖直向下的匀强电场中,场强大小E=5×103N/C,一不带电
下一篇:如图10所示,一质量M=0.8kg的小物块,用长l=0.8m的细绳悬挂在天花板土,处于静止状态.一质量m=0.2kg的橡皮泥粘性小球以速度v0=l0m/s水平射向物块,并与物块粘在一起,小球
零零教育社区:论坛热帖子
|






