在长为2L的绝缘轻质细杆的两端各连接一个质量均为m的带电小球A和B(可视为质点,也不考虑二者间的相互作用力),A球带正电、电荷量为+2q,B球带负电.电荷量为-3q.现把A和B组成
◎ 题目
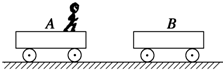
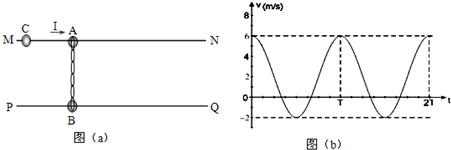
| 在长为2L的绝缘轻质细杆的两端各连接一个质量均为m的带电小球A和B(可视为质点,也不考虑二者间的相互作用力),A球带正电、电荷量为+2q,B球带负电.电荷量为-3q.现把A和B组成的带电系统锁定在光滑绝缘的水平面上,并让A处于如图所示的有界匀强电场区域MPQN内.已知虚线MP是细杆的中垂线,MP和NQ的距离为4L,匀强电场的场强大小为E,方向水平向右.现取消对A、B的锁定,让它们从静止开始运动.(忽略小球运动中所产生的磁场造成的影响) (1)求小球A、B运动过程中的最大速度; (2)小球A、B能否回到原出发点?若不能,请说明理由;若能,请求出经过多长时间带电系统又回到原地发点. (3)求运动过程中带电小球B电势能增加的最大值.  |
◎ 答案
| (1)带电系统开始运动后,向右加速运动;当B进入电场时,开始做减速运动;故在B刚进入电场时,具有最大加速度; 设B进入电场前的过程中,对AB球系统,由动能定理,有 qEL =
解得:v1=
即小球A、B运动过程中的最大速度为
(2)当球A运动到右侧边界过程中,对系统运用动能定理,有 2qE?3L-3qE?2L=
解得 v2=0 由于合力向左,故此后系统回到出发点; 设B从开始到刚进入电场的时间为t1,根据运动学公式,有 v1=a1t1 ② 根据牛顿第二定律,有 2qE=2ma ③ 由①②③解得 t1=
设B进入电场后,系统加速度为a2,由牛顿第二定律,有 -3qE+2qE=2ma2 系统做匀减速运动,减速所需时间为t2,则有t2=
|