如图所示,两个等高的台阶P和Q相距d=4m,台阶面和它们之间的水平地面均光滑.在地面上靠近P台阶处静止有一辆质量为M=2kg的平板小车,车的上表面与台阶面齐平.一质量为m=6kg的
◎ 题目
| 如图所示,两个等高的台阶P和Q相距d=4m,台阶面和它们之间的水平地面均光滑.在地面上靠近P台阶处静止有一辆质量为M=2kg的平板小车,车的上表面与台阶面齐平.一质量为m=6kg的货物(可视为质点)以初速度v0=4m/s在从台阶P冲上小车.货物与平板车之间的摩擦系数为μ=0.2,小车与台阶的碰撞没有机械能损失. (1)若小车与台阶Q第一次碰撞时,货物已经在车的最右端与小车相对静止,求小车的长度L; (2)在第(1)问情况下,货物从离开台阶P到冲上台阶Q所需的时间t; (3)若台阶P、Q间的距离足够长,其他条件不变,要让货物能冲上台阶Q,求小车所有可能的长度. 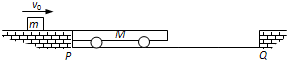 |
◎ 答案
| (1)货物冲上平板车到达到共同速度,以货物与车组成的系统为研究对象,以货物的初速度方向为正方向,由动量守恒定律得: mv0=(M+m)v共1, 由能量守恒定律得:
联立代入数据得:v共1=3m/s,L=1m; (2)货物冲上平板车到达到共同速度,对货物,由动量定理得: -μmgt1=mv共1-mv0 由动能定理得:-μmgx1=
联立并代入数据得:t1=0.5s x1=1.75m, 之后匀运动直至与台阶Q相碰:t2=
从P到Q总用:t=t1+t2=0.5+0.75=1.25s, (3)PQ间距离足够长,货物与小车第一次达到共同速度的值不受影响.v共1=3m/s Q第一次碰后会第二次达到共同速度,以货物初速度方向为正方向,由动量守恒定律得: mv共1-Mv共1=(M+m)v共2 解得:v共2=
小车再与Q碰撞.碰后的情况与之前的情况类似.所以,第n次达到共同速度时:v共n=(
若第n次达到共同速度时,货物恰好出现在小车右端,则货物可以冲上台阶Q. 从冲上小车到冲上Q,整个过程货物只相对小车向右单向运动.对系统 由动能定理得:-μmgL1=
解得:L1=4-
答:(1)小车的长度1m; (2)货物从离开台阶P到冲上台阶Q所需的时间为1.25s; (3)小车所有可能的长度4- |






