如图所示,固定点O上系一长L=0.6m的细绳,细绳的下端系一质量m=1.0kg的小球(可视为质点),原来处于静止状态,球与平台的B点接触但对平台无压力,平台高h=0.80m,一质量M=
◎ 题目
| 如图所示,固定点O上系一长L=0.6m的细绳,细绳的下端系一质量m=1.0kg的小球(可视为质点),原来处于静止状态,球与平台的B点接触但对平台无压力,平台高h=0.80m,一质量M=2.0kg的物块开始静止在平台上的P点,现对M施予一水平向右的初速度V0,物块M沿粗糙平台自左向右运动到平台边缘B处与小球m发生正碰,碰后小球m在绳的约束下做圆周运动,经最高点A时,绳上的拉力恰好等于摆球的重力,而M落在水平地面上的C点,其水平位移S=1.2m,不计空气阻力,g=10m/s2,求: (1)质量为M物块落地时速度大小? (2)若平台表面与物块间动摩擦因数μ=0.5,物块M与小球的初始距离为S1=1.3m,物块M在P处的初速度大小为多少? 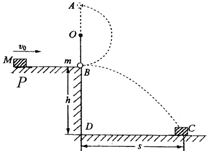 |
◎ 答案
| (1)碰后物块M做平抛运动,设其 平抛运动的初速度为V3 h=
S=V3t …② 得:V3=S
落地时的竖直速度为:Vy=
所以物块落地时的速度大小:V=
(2)物块与小球在B处碰撞,设碰撞前物块的速度为V1,碰撞后小球的速度为V2,由动量守恒定律: MV1=mV2+MV3 …⑥ 碰后小球从B处运动到最高点A过程中机械能守恒,设小球在A点的速度为VA:
小球在最高点时依题给条件有:2mg=m
由⑦⑧解得:V2=6.0 m/s …⑨ 由③⑥⑨得:V1=
物块M从P运动到B处过程中,由动能定理: -μMgS1=
|






