婵犳鍠楅敋闁宦板妼鍗遍柟闂寸劍閸庢垿鏌涜箛鏇炲付闁汇劎鍋撴穱濠囶敍閿濆嫭鍊g紓浣介哺缁诲嫭绂掗敂鑺ョ秶闁靛à鈧敃鍌涚厽妞ゅ繐瀚峰Σ鎼佹煕閵忥紕鍙€闁硅櫕娲栭~婵嬪Ψ閵忕姳澹曢梺绋挎湰娓氭宕曞鈧濠氬磼閵堝懏鐏曞銈冨灪閸ㄥ墎绮嬪澶婁紶闁告洦鍋嗛宀勬⒒娓氬洤寮跨紓宥佸亾缂備焦姊婚崰鏍极瀹ュ鍋勯柣鎴炨缚閻f娊姊哄ú璁虫捣闁稿鍔曢埢鏃堝煛閸涱喖鍓梺鍓插亝缁诲秴危闁秵鐓忛柛鈩冾殔閳ь剝顫夐弲鍫曟偐閾忣偄寮块柣搴秵閸犳帡宕戦幘瀛樺閻熸瑥瀚呭杈ㄥ枑闁绘鐗嗛柌婊呯磼鏉堛劎绠炵€规洩缍佸畷濂稿Ψ閵忕姳澹曟繛杈剧到閹诧繝宕戝Ο鍏煎枑闁绘鐗嗙粭鎺擃殽閻愬瓨宕屽┑鈩冩尦瀹曟帒鈹戦崱鈺€鎴烽梻浣告啞鐢偞鏅跺Δ鍛創婵炲棙鎸哥涵鈧┑掳鍊曠€氼剟宕规担绯曟闁瑰墽顒查弨缁樹繆瀹割喖澧撮柡浣哥Ф娴狅箓鎸婃径宀嬬礋濠电偞鍨堕幐绋棵洪妶澶婄濞村吋娼欓崣濠囨煏婢跺牆鈧绮旈崼鏇熺厪闁糕槅鍘界€氾拷
一质量为m、电荷量+q的与外界绝缘物块A(可视为质点),置于光滑水平面上.A与弹簧左端相连接,弹簧右端固定在竖直墙面上,整个空间中存在水平向右的匀强电场,场强为E,平衡时

◎ 题目
一质量为m、电荷量+q的与外界绝缘物块A(可视为质点),置于光滑水平面上.A与弹簧左端相连接,弹簧右端固定在竖直墙面上,整个空间中存在水平向右的匀强电场,场强为E,平衡时弹簧的压缩量为x0,如图O为弹簧原长时的位置,另一个质量也为m电量为+2q的绝缘带电物块B(可视为质点),从O点左侧距离O为7x0处的p点由静止释放,当它打在A物块上时立即与A一起向右运动,但不粘连,它们到达最右端后又向左运动,试求:物块B向左运动达到最远点时距O点的距离?(A、B相撞在瞬间完成,电荷无转移,不计A、B间库仑力,弹簧始终在弹性限度内).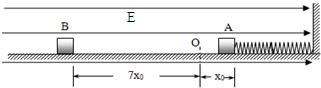 |
◎ 答案
| 对A受力分析:qE=kx0 解得:k=
对B,由动能定理得: 2qE?8x0=
解得:v=4
对B、A碰撞过程,规定向右为正方向,由动量守恒,得到: mv=2mv共 解得:v共=2
寻找分开的位置: 刚分开时物体A与B间的弹力为零且aB=aA; 对A受力分析,受电场力和弹簧的弹力(设为拉力),有: qE+kx=maA 对B受力分析,只受电场力,有: 2qE=maB 解得:x=
故分离点是弹簧伸长x0位置; 从A、B共速后到分开,由动能定理: W电=Ek分-Ek共 即-3qE(x+x0)=
解得:v分=
|







