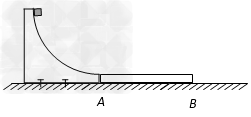
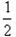如图所示,一质量M=2.0kg的长木板AB静止在水平面上,木板的左侧固定一半径R=0.60m的四分之一圆弧形轨道,轨道末端的切线水平,轨道与木板靠在一起,且末端高度与木板高度相
◎ 题目
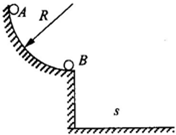
| 如图所示,一质量M=2.0kg的长木板AB静止在水平面上,木板的左侧固定一半径R=0.60m的四分之一圆弧形轨道,轨道末端的切线水平,轨道与木板靠在一起,且末端高度与木板高度相同。现在将质量m=1.0kg的小铁块(可视为质点)从弧形轨道顶端由静止释放,小铁块到达轨道底端时的速度v0=3.0m/s,最终小铁块和长木板达到共同速度。忽略长木板与地面间的摩擦。取重力加速度g=10m/s2。求 (1)小铁块在弧形轨道末端时所受支持力的大小F; (2)小铁块在弧形轨道上下滑过程中克服摩擦力所做的功Wf; (3)小铁块和长木板达到的共同速度v。 |
 |
◎ 答案
解:(1)小木块在弧形轨道末端时,满足 解得:  (2)根据动能定理  解得:  (3)根据动量守恒定律 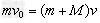 解得:  |
◎ 解析
“略”◎ 知识点
专家分析,试题“如图所示,一质量M=2.0kg的长木板AB静止在水平面上,木板的左侧固定一半径R=0.60m的四分之一圆弧形轨道,轨道末端的切线水平,轨道与木板靠在一起,且末端高度与木板高度相…”主要考查了你对 【向心力】,【动能定理】,【动量守恒定律的应用】 等知识点的理解和应用能力。关于这些知识点的“档案”,你可以点击相应的链接进行查看和学习。- 最新内容
- 相关内容
- 网友推荐
- 图文推荐
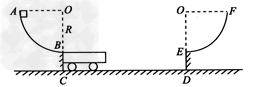
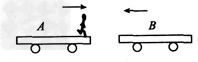
上一篇:如图所示,在竖直面内有一个光滑弧形轨道,其末端水平,且与处于同一竖直面内光滑圆形轨道的最低端相切,并平滑连接。A、B两滑块(可视为质点)用轻细绳拴接在一起,在它们中间
下一篇:如图所示,一个半径为R=1.00m粗糙的14圆弧轨道,固定在竖直平面内,其下端切线是水平的,轨道下端距地面高度h=1.25m.在轨道末端放有质量为mB=0.30kg的小球B(视为质点),B
零零教育社区:论坛热帖子
| [高考] 2022 西安电子科技大学《软件工程》大作业答案 (2022-04-25) |
| [家长教育] 孩子为什么会和父母感情疏离? (2019-07-14) |
| [教师分享] 给远方姐姐的一封信 (2018-11-07) |
| [教师分享] 伸缩门 (2018-11-07) |
| [教师分享] 回家乡 (2018-11-07) |
| [教师分享] 是风味也是人间 (2018-11-07) |
| [教师分享] 一句格言的启示 (2018-11-07) |
| [教师分享] 无规矩不成方圆 (2018-11-07) |
| [教师分享] 第十届全国教育名家论坛有感(二) (2018-11-07) |
| [教师分享] 贪玩的小狗 (2018-11-07) |