某兴趣小组设计了一种实验装置,用来研究碰撞问题,其模型如图所示不用完全相同的轻绳将N个大小相同、质量不等的小球并列悬挂于一水平杆、球间有微小间隔,从左到右,球的编
◎ 题目
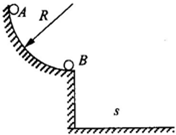
| 某兴趣小组设计了一种实验装置,用来研究碰撞问题,其模型如图所示不用完全相同的轻绳将N个大小相同、质量不等的小球并列悬挂于一水平杆、球间有微小间隔,从左到右,球的编号依次为1、2、3…N,球的质量依次递减,每球质量与其相邻左球质量之比为k(k<1).将1号球向左拉起,然后由静止释放,使其与2号球碰撞,2号球再与3号球碰撞…所有碰撞皆为无机械能损失的正碰.(不计空气阻力,忽略绳的伸长,g取10m/s2) (1)设与n+1号球碰撞前,n号球的速度为vn,求n+1号球碰撞后的速度. (2)若N=5,在1号球向左拉高h的情况下,要使5号球碰撞后升高16k(16h小于绳长)问k值为多少? 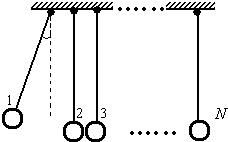 |
◎ 答案
| (1)本题中的两球相碰,均可看成是“一静一动弹性碰撞模型”.因为每个球的质量依次递减,碰后不会出现入射球反弹的情况.如果入射球质量为m1,被碰球质量为m2,碰前m1的速度为v1,碰后两球的速度分别为v1′、v2′由动量守恒定律和机械能守恒定律得: m v1=m1v1′+m2v2′
得:V′1=
本题主要应用v2′当n取代1时,n+1就取代2. 设n号球质量为m,与n+1号球碰撞后的速度分别为vn′、vn+1′取水平向右为正方向,据题意有n号球与n+1号球碰撞前的速度分别为vn、0、mn+1=kmn 根据动量守恒,有mnVn=mnV′n+kmnV′n+1…① 根据机械能守恒,有
由①②得:V′n+1=
(2)设1号球摆至最低点时的速度为v1,由机械能守恒定律有: m1gh=
v
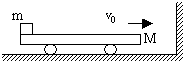
上一篇:水平光滑的地面上,质量为m的木块放在质量为M的平板小车的左端,M>m,它们一起以大小为v0的速度向右做匀速直线运动,木块与小车之间的动摩擦因数为μ,小车与竖直墙碰后立即以
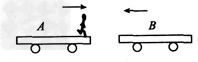
下一篇:木块B与水平桌面间的接触是光滑的,子弹A沿水平方向射入木块后留在木块内,将弹簧压缩到最短。现将子弹、木块和弹簧合在一起作研究对象,则此系统在从子弹开始射入木块到弹簧
零零教育社区:论坛热帖子
|