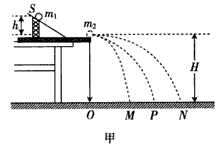
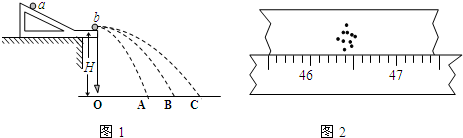
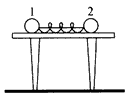
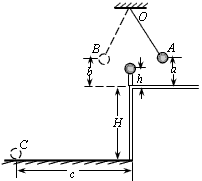
用如图所示装置来验证动量守恒定律.质量为mA的钢球A用细线悬挂于O点,质量为mB的钢球B放在离地面高度为H的小支柱N上,O点到A球球心的距离为L,使悬线在A球释放前伸直,且线与
◎ 题目
| 用如图所示装置来验证动量守恒定律.质量为mA的钢球A用细线悬挂于O点,质量为mB的钢球B放在离地面高度为H的小支柱N上,O点到A球球心的距离为L,使悬线在A球释放前伸直,且线与竖直线夹角为α,A球释放后摆到最低点时恰与B球正碰,碰撞后,A球把轻质指示针OC推移到与竖直线夹角β处,B球落到地面上,地面上铺有一张盖有复写纸的白纸D,保持α角度不变,多次重复上述实验,白纸上记录到多个B球的落点.(已知当地的重力加速度为g) (1)为验证两球碰撞过程动量守恒,应测出数值的物理量有S以及______.(用题中字母表示) (2)用测得的物理量表示碰撞前后A球、B球的动量:PA=______,PA′=______.PB=0,PB′=______. 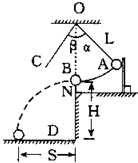 |
◎ 答案
| (1)实验过程中需要求出两小球碰撞前后的动量,因此需要知道小球的质量与速度,小球的速度可以由动能定理与平抛运动知识求得,因此该实验需要测量的物理量有:小球的质量mA、mB,倾角α与β,球B飞出时的高度H,绳长L;即需要测量的量有:mA、mB、α、β、H、L. (2)小球从A处下摆过程只有重力做功,机械能守恒,由机械能守恒定律得: mAgL(1-cosα)=
小球A与小球B碰撞后继续运动,在A碰后到达最左端过程中,机械能再次守恒, 由机械能守恒定律得:-mAgL(1-cosβ)=0-
PA′=mAvA′=mA
碰撞后B球做平抛运动,水平方向:S=vB′t,竖直方向H=
解得vB′=S
故答案为:(1)mA、mB、α、β、H、L;(2)mA |