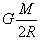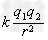如图所示,固定于同一条竖直线上的A、B是两个带等量异种电荷的点电荷,电荷量分别为+Q和-Q,A、B相距为2d.MN是竖直放置的光滑绝缘细杆,另有一个穿过细杆的可视为点电荷的带
◎ 题目
| 如图所示,固定于同一条竖直线上的A、B是两个带等量异种电荷的点电荷,电荷量分别为+Q和-Q,A、B相距为2d.MN是竖直放置的光滑绝缘细杆,另有一个穿过细杆的可视为点电荷的带电小球,质量为m、电荷量为+q,(此电荷不影响电场的分布.),现将小球从与点电荷A等高的C处由静止开始释放,小球向下运动到O点时速度为v,已知CO=d,MN与AB之间的距离为d,静电力常量为k,重力加速度为g. 求: (1)C、O间的电势差U; (2)O点处的电场强度E的大小; (3)小球经过与点电荷B等高的D点时的速度. 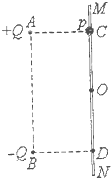 |
◎ 答案
| (1)小球p由C运动到O时,由动能定理, 得:mgd+qUC0=
∴UCO=
(2)小球p经过O点时受力分析, 由库仑定律得:F1=F2=k
它们的合力为:F=F1cos45°+F2cos45°=
∴O点处的电场强度E=
(3)小球p由O运动到D的过程,由动能定理得:mgd+qUOD=
由电场特点可知:UCO=UOD ⑥ 联立①⑤⑥解得:vD=
答:(1)C、O间的电势差UCO是
(2)O点处的电场强度E的大小是 |

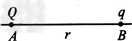
![两个完全相同的金属小球,所带异种电荷的电量之比为3:5,当它们相距L(L远大于小球大小)时,相互作用力为F,现将两球接触后放到相距为2L的两点,这时两球相互作用力大小是[]A](http://www.00-edu.com/d/file/2022-11-28/00317c57eb7bb4c6b873661d450dd5d4.gif)