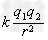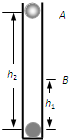
如图所示，一个内壁光滑的绝缘细直管竖直放置．在管子的底部固定一电荷量为Q（Q＞0）的带电体．在距离底部点电荷为h2的管口A处，有一电荷量为q（q＞0）、质量为m的小球自静止释放，在
◎ 题目
如图所示，一个内壁光滑的绝缘细直管竖直放置．在管子的底部固定一电荷量为Q（Q＞0）的带电体．在距离底部点电荷为h2的管口A处，有一电荷量为q（q＞0）、质量为m的小球自静止释放，在距离底部点电荷为h1的B处速度恰好为零．现让一个电荷量为q、质量为2m的小球仍在A处自静止释放，已知静电力常量为k，重力加速度为g，则该小球（ ）
 |
◎ 答案
| A、质量为m点电荷A，从静止释放后开始下落，库仑力越来越大，所以点电荷先加速后减速．则加速度先减小后增大．当到达B点时，点电荷A停止．由动能定理可得：mg（h2-h1）-W库=0-0 W库=mg（h2-h1） 而当换成质量2m点电荷A′时，仍从原来位置静止释放，则点电荷先加速后减速．则加速度先减小后增大． 设停止的位置为B′，则由动能定理可得：2mg（h2-h1′）-W库=0-0 所以h2-h1′=
B、而当换成质量2m点电荷A′时，仍从原来位置静止释放，则点电荷先加速后减速．则加速度大小先减小后增大．故B正确； C、速度最大位置，就是加速度为零的位置．即库仑力与重力相等的位置． 当质量为m 时，设平衡位置距点电荷B的距离为h0 则有：k
而当质量为2m时，设平衡位置距底部点电荷的距离为h0′则有：k
所以h0′=
|
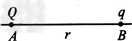
![两个完全相同的金属小球，所带异种电荷的电量之比为3：5，当它们相距L（L远大于小球大小）时，相互作用力为F，现将两球接触后放到相距为2L的两点，这时两球相互作用力大小是[]A](http://www.00-edu.com/d/file/2022-11-28/00317c57eb7bb4c6b873661d450dd5d4.gif)
