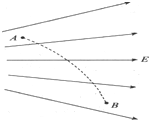
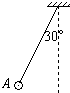
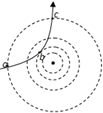
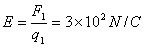绝缘细绳的一端固定在天花板上,另一端连接着一个带负电的电量为q、质量为m的小球,当空间建立水平方向的匀强电场后,绳稳定处于与竖直方向成θ=600角的位置,如图所示.(1)求
◎ 题目
| 绝缘细绳的一端固定在天花板上,另一端连接着一个带负电的电量为q、质量为m的小球,当空间建立水平方向的匀强电场后,绳稳定处于与竖直方向成θ=600角的位置,如图所示. (1)求匀强电场的场强E; (2)若细绳长为L,让小球从θ=30°的A点释放,王明同学求解小球运动至某点的速度的过程如下: 据动能定理-mgL(1-cos30°)+qELsin30°=
 |
◎ 答案
| (1)小球在θ=600角处处于平衡,根据平衡条件得: 则Eq=mgtanθ  得E=
方向水平向左 (2)王明同学的求解不正确. 因为小球在θ=600处处于平衡,因此小球从θ=300的A点释放,它不会往A点的左边运动,而是以θ=600处为中心、以A点为端点来回摆动,即小球不会运动至最低点O. 王明同学的求解实际上也不是小球运动到θ=600的平衡位置处的速度. 平衡位置处的速度的正确求解应该是:据动能定理有 qE(Lsin60°-Lsin30°)-mg(Lcos30°-Lcos60°)=
联解得:v=(
答:(1)匀强电场的场强大小是
(2)王明同学的求解不正确.平衡位置处的速度是( |