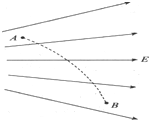
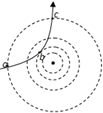
在光滑水平面上固定一个竖直圆筒S,圆筒内壁光滑(如图所示为俯视图),半径为1m.圆筒圆心O处用一根不可伸长的长0.5m的绝缘细线系住一个质量为0.2kg,电量为+5×10-5C的小球,
◎ 题目
| 在光滑水平面上固定一个竖直圆筒S,圆筒内壁光滑(如图所示为俯视图),半径为1m.圆筒圆心O处用一根不可伸长的长0.5m的绝缘细线系住一个质量为0.2kg,电量为+5×10-5C的小球,小球体积忽略不计.水平方向有一匀强电场E=4×104N/C,方向如图所示.小球从图示位置(细线和电场线平行)以vo=10m/s垂直于场强方向运动.当细线转过900时,细线突然断裂.求: (1)细线断裂时小球的速度大小; (2)小球碰到圆筒内壁后不反弹,沿圆筒内壁继续做圆周运动中的最小速度值; (3)现在圆心O处用一根牢固的不可伸长的长为0.5m的绝缘细线系住小球(小球质量和带电量均不变),小球从原图示位置以初速度10m/s垂直于场强方向运动,为保证小球接下来的运动过程中细线都不松弛,电场强度E的大小范围(场强方向不变).  |
◎ 答案