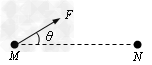
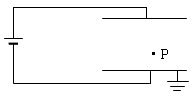
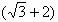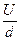如图所示,可视为质点的三物块A、B、C放在倾角为30°、长L=2m的固定斜面上,物块与斜面间的动摩擦因数μ=7380,A与B紧靠在一起,C紧靠在固定挡板上,三物块的质量分别为mA=0.
◎ 题目
如图所示,可视为质点的三物块A、B、C放在倾角为30°、长L=2m的固定斜面上,物块与斜面间的动摩擦因数μ=
(1)未施加拉力F时物块B、C间的距离; (2)t0时间内A上滑的距离及库仑力做的功; (3)拉力F对A物块做的总功.  |
◎ 答案
(1)A、B、C处于静止状态时,设B、C间距离为L1,则C对B的库仑斥力:F0=
以A、B为研究对象,根据力的平衡 F0=(mA+mB)gsin30° 联立解得 L1=1.0m (2)给A施加力F后,A、B沿斜面向上做匀加速直线运动,C对B的库仑斥力逐渐减小,A、B之间的弹力也逐渐减小.经过时间t0,B、C间距离设为L2,A、B两者间弹力减小到零,此后两者分离,力F变为恒力.则t0时刻C对B的库仑斥力为:F0=
以B为研究对象,由牛顿第二定律有:F0-mBgsin30°-μmBgcos30°=mBa ② 联立①②解得 L2=1.2m 则t0时间内A上滑的距离△L=L2+L1=0.2m 设t0时间内库仑力做的功为W0,由功能关系有 W0=k
代入数据解得 W0=1.2J ③ (3)设在t0时间内,末速度为v1,力F对A物块做的功为W1,由动能定理有 W1+W2+WG+Wf=
|