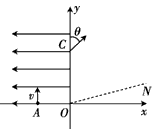
在如图所示的直角坐标中,x轴的上方有与x轴正方向成45°角的匀强电场,场强的大小为E=2×104V/m.x轴的下方有垂直于xOy面的匀强磁场,磁感应强度的大小为B=2×10-2T,方向垂直于
◎ 题目
在如图所示的直角坐标中,x轴的上方有与x轴正方向成45°角的匀强电场,场强的大小为E=
①电荷从释放到第一次进入磁场时所用的时间t; ②电荷在磁场中的偏转半径; ③电荷第二次到达x轴上的位置. 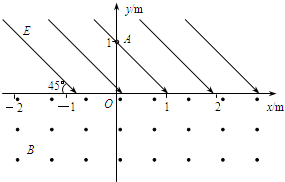 |
◎ 答案
(1)带电粒子从A点出发,至第一次到x轴为第一过程,在这个过程中,带电粒子做匀加速直线运动,位移大小由图中的直角三角形可以解出x=
由匀变速直线运动的位移时间关系式:x=
整理得:t=
(2)粒子到达磁场时的速度:v=at=
根据洛伦兹力提供向心力:qvB=
解得:R=
(3)带电粒子在磁场中的运动轨迹如图所示: 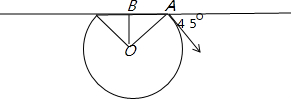 在直角三角形OAB中:AB=Rsin45°=
所以粒子再次到达x轴时距离A点左方2AB即1m处,所以电荷第二次到达x轴上的位置为(0,0). 故答案为: ①电荷从释放到第一次进入磁场时所用的时间为10-6s; ②电荷在磁场中的偏转半径 |