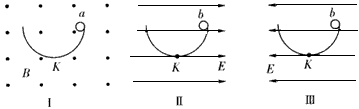
如图所示,空间分布着有理想边界的匀强电场和匀强磁场,已知左侧匀强电场的场强大小为E、方向水平向右,其宽度为L;中间区域匀强磁场的磁感应强度大小为B、方向垂直纸面向外
◎ 题目
| 如图所示,空间分布着有理想边界的匀强电场和匀强磁场,已知左侧匀强电场的场强大小为E、方向水平向右,其宽度为L;中间区域匀强磁场的磁感应强度大小为B、方向垂直纸面向外;右侧匀强磁场的磁感应强度大小也为B、方向垂直纸面向里.一个带正电的粒子(质量为m、电荷量为q,不计重力)从电场左边缘a点由静止开始运动,穿过中间磁场区域进入右侧磁场区域后,又回到了a点,然后重复上述运动过程.求: (1)中间磁场区域的宽度d. (2)带电粒子从a点开始运动到第一次回到a点时所用的时间t.  |
◎ 答案
(1)电场中加速过程,根据动能定理,有:qEL=
粒子在两磁场中做匀速圆周运动,洛伦兹力提供向心力,根据牛顿第二定律,有: qvB=m
 画出粒子的运动轨迹,如图所示,三段圆弧的圆心构成的三角形是等边三角形,变成为2r; 故中间磁场的宽度为:d=rsin60°=
(2)粒子在电场中做匀变速直线运动,加速阶段由运动学公式L=
|