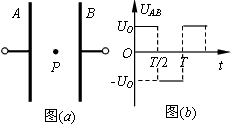
如图(a)所示,电子从加速电场的O点发出(初速不计),经电压为U1的加速电场加速后沿中心线进入两平行金属板M、N间的匀强电场中,通过电场后打到荧光屏上的P点处,设M、N板间的
L1v0
=
cm=2.25cm
从偏转电场出来后作直线运动:由
=
得Y=
y=
×2.25cm=18cm
[或直接求Y=(L2+
)tanθ=(21+3)×
cm=18cm]
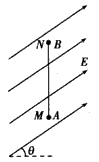
(3)如图乙所示,电子轨迹从磁场出来的切线延长线交于磁场区的圆心,因为也打在P点,所以θ=37°
由图可知电子轨道半径R满足:
Rsinθ=
+
cosθ
解之得:
R=
=
cm=9cm
又R=
得B=
=
| U2L1 |
| 4U1 |
| 300×6 |
| 4×200 |
从偏转电场出来后作直线运动:由
| Y |
| y |
| ||
|
得Y=
| L1+2L2 |
| L1 |
| 6+2×21 |
| 6 |
[或直接求Y=(L2+
| L1 |
| 2 |
| 3 |
| 4 |
(3)如图乙所示,电子轨迹从磁场出来的切线延长线交于磁场区的圆心,因为也打在P点,所以θ=37°
由图可知电子轨道半径R满足:
Rsinθ=
| L1 |
| 2 |
| L1 |
| 2 |
解之得:
R=
| L1(1+cosθ) |
| 2sinθ |
| 6×(1+0.8) |
| 2×0.6 |
又R=
| mv0 |
| eB |
得B=
| mv0 |
| eR |