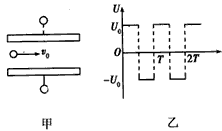
两块足够大的平行金属板水平放置,极板间加有空间分布均匀、大小随时间周期性变化的电场和磁场,变化规律分别如图1、图2所示(规定垂直纸面向里为磁感应强度的正方向).在t=0时
◎ 题目
两块足够大的平行金属板水平放置,极板间加有空间分布均匀、大小随时间周期性变化的电场和磁场,变化规律分别如图1、图2所示(规定垂直纸面向里为磁感应强度的正方向).在t=0时刻由负极板释放一个初速度为零的带负电的粒子(不计重力).若电场强度E0、磁感应强度B0、粒子的比荷q/m均已知,且t0=
 (1)求粒子在0~t0时间内的位移大小与极板间距h的比值. (2)求粒子在两极板间做圆周运动的最大半径(用h表示). (3)若板间电场强度E随时间的变化仍如图1所示,磁场的变化改为如图3所示,试画出粒子在板间运动的轨迹图(不必写计算过程). |
◎ 答案
解法一: (1)设粒子在0~t0时间内的位移大小为s1,由运动学公式和你对第二定律有: s1=
又已知t0=
联立以上两式解得:
(2)粒子在t0~2t0时间内只受洛伦兹力作用,且速度与磁场方向垂直,所以粒子做匀速圆周运动.设运动速度大小为v1,轨道半径为R1,周期为T,则有: v1=at0,qv1B0=
联立以上两式得R1=
又T=
s2=v1t0+ |