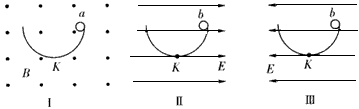
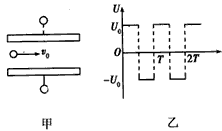
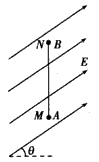
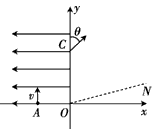
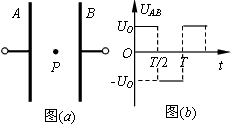
两块足够大的平行金属板水平放置,极板间加有空间分布均匀、大小随时间周期性变化的电场和磁场,变化规律分别如图1、图2所示(规定垂直纸面向里为磁感应强度的正方向).在t=0时
| t | 20 |
解得:s2=
| 3 |
| 5 |
由于s1+s2<h,所以粒子在3t0~4t0时间内继续做匀速圆周运动,设速度大小为v2,半径为R2,则有:
v2=v1+at0,qv2B0=
m
| ||
| R2 |
解得:R2=
| 2h |
| 5π |
由于s1+s2+R2<h,粒子恰好又能完成一个周期的圆周运动.
在4t0~5t0时间内,粒子运动到正极板(如图1所示).因此粒子的最大半径为:

R2=
| 2h |
| 5π |
(3)粒子在板间运动的轨迹如图2所示.
解法二:
由题意可知,电磁场的周期为2t0,前半周期粒子受电场作用做匀加速直线运动,加速度大小为:
a=
| qE0 |
| m |
后半周期粒子受磁场作用多匀速圆周运动,周期为T,则有:
T=
| 2πm |
| qB0 |
粒子恰好完成一次匀速圆周运动.至第n个周期末,粒子位移大小为sn,有:
sn=
| 1 |
| 2 |
又已知sn=
| n |
| 5π |
粒子速度大小为vn=ant0,粒子做圆周运动的半径为:
Rn=
| mvn |
| qB0 |
解得:Rn=
| nh |
| 5π |
所以有:(1)粒子在0~t0时间内的位移大小与极板间距h的比值为
| s1 |
| h |
| 1 |
| 5 |
(2)粒子在两极板间做圆周运动的最大半径R2=
| 2h |
| 5π |
(3)粒子在板间运动的轨迹图见解法一中的图2.
答:(1)粒子在0~t0时间内的位移大小与极板间距h的比值为
| s1 |
| h |