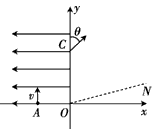
如图所示的平面直角坐标系中,虚线OM与x轴成45°角,在OM与x轴之间(包括x轴)存在垂直纸面向里、磁感应强度大小为B的匀强磁场,在y轴与OM之间存在竖直向下、电场强度大小为E的
◎ 题目
| 如图所示的平面直角坐标系中,虚线OM与x轴成45°角,在OM与x轴之间(包括x轴)存在垂直纸面向里、磁感应强度大小为B的匀强磁场,在y轴与OM之间存在竖直向下、电场强度大小为E的匀强电场,有一个质量为m,电荷量为q的带正电的粒子以某速度沿x轴正方向从O点射入磁场区域并发生偏转,不计带电粒子的重力和空气阻力,在带电粒子进入磁场到第二次离开电场的过程中,求 (1)若带电粒子从O点以速度V1进入磁场区域,求带电粒子第一次离开磁场的位置到O点的距离? (2)若带电粒子第二次离开电场时恰好经过O点,求粒子最初进入磁场时速度V的大小?并讨论当V变化时,粒子第二次离开电场时速度大小与V大小的关系. 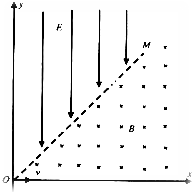 |
◎ 答案
 (1)带电粒子进入磁场中,受到洛伦兹力做匀速圆周运动,由牛顿第二定律得 qv1B=m
得轨迹半径 R=
设粒子从N点离开磁场,如图,由几何知识知,ON=
(2)带电粒子进入电场时做类平抛运动,第二次离开电场时恰好经过O点,画出轨迹,则 水平位移 x=2R=vt 竖直位移 y=2R=
而a=
联立得:v=
讨论: i)若v>
离开电场时竖直分速度vy=at=
带电粒子离开电场时速度大小为u= |