两根足够长的光滑平行直导轨MN、PQ与水平面成θ角放置,两导轨间距为L,M、P两点间接有阻值为R的电阻.一根质量为m的均匀直金属杆ab放在两导轨上,并与导轨垂直.整套装置处于磁
◎ 题目
| 两根足够长的光滑平行直导轨MN、PQ与水平面成θ角放置,两导轨间距为L,M、P两点间接有阻值为R的电阻.一根质量为m的均匀直金属杆ab放在两导轨上,并与导轨垂直.整套装置处于磁感应强度为B的匀强磁场中,磁场方向垂直于导轨平面向上,导轨和金属杆接触良好,它们的电阻不计.现让ab杆由静止开始沿导轨下滑. (1)求ab杆下滑的最大速度vm; (2)ab杆由静止释放至达到最大速度的过程中,电阻R产生的焦耳热为Q,求该过程中ab杆下滑的距离x及通过电阻R的电量q. 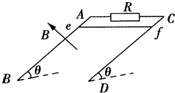 |
◎ 答案
| (1)根据法拉第电磁感应定律和安培力公式有: E=BLv ① I=
FA=BIL ③ 根据牛顿第二定律有: mgsinθ-FA=ma ④ 联立①②③④得:mgsinθ-
当加速度a为零时,速度v达最大,速度最大值:vm=
故ab杆下滑的最大速度为vm=
(2)根据能量守恒定律有: mgxsinθ=
得x=
根据电磁感应定律有:
根据闭合电路欧姆定律有:
感应电量: q=
得:q=
|

![用比值法定义物理量是物理学中一种常用的方法,下面四个物理量都是用比值法定义的。以下公式不属于定义式的是[]A.电流强度B.磁感应强度C.电场强度D.电阻](http://www.00-edu.com/d/file/2022-12-09/73c8028def55e19f2c80c7070bb6b703.gif)
![如图所示电路,电压保持不变,当电键S断开时,电流表A的示数为0.6A,当电键S闭合时,电流表的示数为0.9A,则两电阻阻值之比R1:R2为[]A.1:2B.2:1C.2:3D.3:2](http://www.00-edu.com/d/file/2022-12-09/bb95673d0aa4a57aeaab1d96dcc36e91.gif)
