如图所示,光滑的平行金属导轨CD与EF间距为L=lm,与水平夹角为θ=30°,导轨上端用导线CE连接(导轨和连接线电阻不计),导轨处在磁感应强度为B=0.1T、方向垂直于导轨平面向上的
| x |
则得kgsinθ-
B2L2
| ||
| R |
从上述方程可以看出的解ax是一个定值,与位移x无关,这表明前面的假设成立,棒的运动确实是匀加速直线运动.若ax与位移x有关,则说明ax是一个变量,即前面的假设不成立.
(3)为了求棒下滑2m时的速度,应先求出棒的加速度.将题目给出的数据代①式得到
0.1×10×
| 1 |
| 2 |
| ||
| 1 |
| a |
化简得 10a+
| 2 |
| a |
令y=
| a |
| 2 |
解得,a=4.69m/s2
根据匀变速运动规律,v=
| 2axx |
|
上一篇:如图所示,是用直流电动机提升重物的装置示意图,电源电动势E=100V,内电阻r1=1Ω,电动机的线圈电阻r2=4Ω.重物质量m=36kg,重物被电动机以v=0.5m/s的速度匀速提起,不计重物
下一篇:如图(a)所示,两根足够长的光滑水平金属导轨相距为L=0.40m,导轨平面与水平面成θ=30°角,上端和下端通过导线分别连接阻值R1=R2=1.2Ω的电阻,质量为m=0.20kg、阻值r=0.20
零零教育社区:论坛热帖子
|

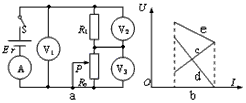
![调整如图所示电路的可变电阻R的阻值,使电压表V的示数增大ΔU,在这个过程中[]A.通过R1的电流增加,增加量一定等于ΔU/R1B.R2两端的电压减小,减少量一定等于ΔUC.通过R2的](http://www.00-edu.com/d/file/2022-12-16/4b672f344d573f257757d3bc171056a7.gif)
![如图所示的电路,闭合开关S,当滑动变阻器滑片p向右移动时,下列说法正确的是[]A.电流表读数变小,电压表读数变大B.小电泡L变暗C.电容器C上电荷量减小D.电源的总功率变小](http://www.00-edu.com/d/file/2022-12-16/2dc51b52acf3dcda28e2e7dd1a3dccd8.gif)
![如图所示电路的电源内阻不可忽略,若调整可变电阻R的阻值,可使电压表V的示数增大△U(电压表为理想电表),在这个过程中[]A.通过R1的电流增加,增加量一定等于△U/R1B.R2两端的](http://www.00-edu.com/d/file/2022-12-16/325f720d2726b0512a35cf546ebc1bfc.gif)
