如图(a)所示,在坐标平面xOy内存在磁感应强度为B=2T的匀强磁场,OA与OCA为置于竖直平面内的光滑金属导轨,其中OCA满足曲线方程x=0.5sin(π3y)m,C为导轨的最右端,导轨OA与O
◎ 题目
如图(a)所示,在坐标平面xOy内存在磁感应强度为B=2T的匀强磁场,OA与OCA为置于竖直平面内的光滑金属导轨,其中OCA满足曲线方程x=0.5sin(
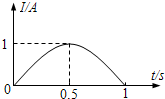
(1)金属棒MN在导轨上运动时感应电动势的最大值; (2)请在图(b)中画出金属棒MN中的感应电流I随时间t变化的关系图象; (3)当金属棒MN运动到y=2.5m处时,外力F的大小; (4)若金属棒MN从y=0处,在不受外力的情况下,以初速度v=6m/s向上运动,当到达y=1.5m处时,电阻R1的瞬时电功率为P1=0.9W,在该过程中,金属棒克服安培力所做的功. 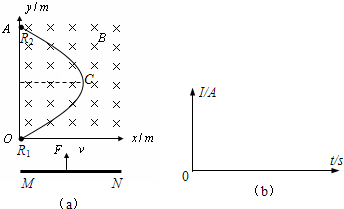 |
◎ 答案
 (1)当金属棒MN匀速运动到C点时,电路中感应电动势最大 金属棒MN接入电路的有效长度为导轨OCA形状满足的曲线方程中的x值. 因此接入电路的金属棒的有效长度为L=x=0.5sin
则有.Lm=xm=0.5m 感应电动势,Em=BLmv 解得:Em=3.0V (2)闭合电路欧姆定律,Im=
且R总=
解得:Im=1.0A, 如图所示, (3)金属棒MN匀速运动中受重力mg、安培力F安、外力F外作用 当y=2.5m时,x=0.5sin
受力平衡,F外=F安+mg=BIL+mg=
(4)当y=1.5m时,x=0.5sin
此时P1=0.9W,所以P总=
P总=F安v=
得此时vt2=3.6(m/s)2 选取从y=0处到达y=1.5m处时,根据动能定理,则有:W克= |

![调整如图所示电路的可变电阻R的阻值,使电压表V的示数增大ΔU,在这个过程中[]A.通过R1的电流增加,增加量一定等于ΔU/R1B.R2两端的电压减小,减少量一定等于ΔUC.通过R2的](http://www.00-edu.com/d/file/2022-12-16/4b672f344d573f257757d3bc171056a7.gif)
![如图所示的电路,闭合开关S,当滑动变阻器滑片p向右移动时,下列说法正确的是[]A.电流表读数变小,电压表读数变大B.小电泡L变暗C.电容器C上电荷量减小D.电源的总功率变小](http://www.00-edu.com/d/file/2022-12-16/2dc51b52acf3dcda28e2e7dd1a3dccd8.gif)
![如图所示电路的电源内阻不可忽略,若调整可变电阻R的阻值,可使电压表V的示数增大△U(电压表为理想电表),在这个过程中[]A.通过R1的电流增加,增加量一定等于△U/R1B.R2两端的](http://www.00-edu.com/d/file/2022-12-16/325f720d2726b0512a35cf546ebc1bfc.gif)
