如图甲，在水平桌面上固定着两根相距0.2m,相互平行的无电阻轨道P和轨道一端固定一根电阻为0.0lΩ的导体棒a，轨道上横置一根质量为40g、电阻为0.0lΩ的金属棒b，两棒相距0.-00教育-零零教育信息网

如图甲，在水平桌面上固定着两根相距0.2m,相互平行的无电阻轨道P和轨道一端固定一根电阻为0.0lΩ的导体棒a，轨道上横置一根质量为40g、电阻为0.0lΩ的金属棒b，两棒相距0.

首页 > 考试 > 物理 > 高中物理 > 磁场对通电导线的作用：安培力、左手定则/2023-04-06 / 加入收藏 / 阅读 [打印]

◎ 题目

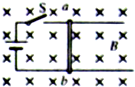
如图甲，在水平桌面上固定着两根相距0.2m,相互平行的无电阻轨道P和轨道一端固定一根电阻为0.0l Ω的导体棒a，轨道上横置一根质量为40g、电阻为0.0lΩ的金属棒b，两棒相距0.2m．该轨道平面处在磁感应强度大小可以调节的竖直向上的匀强磁场中．开始时，磁感应强度B₀="0.10" T(设棒与轨道间的最大静摩擦力和滑动摩擦力相等，g取10 m/s²)

（1）若从t=0开始，磁感应强度B随时间t按图乙中图象所示的规律变化，求在金属棒b开始运动前，这个装置释放的热量是多少?
（2）若保持磁感应强度B₀的大小不变，从t=0时刻开始，给b棒施加一个水平向右的拉力，使它做匀加速直线运动．此拉力F的大小随时间t变化关系如图丙所示．求匀加速运动的加速度及b棒与导轨间的滑动摩擦力．

◎ 答案

（1）0.036J（2）a=5m/s² f=0.2N

◎ 解析

试题分析：(1)当磁感应强度均匀增大时，闭合电路中有恒定的感应电流I，以b棒为研究对象，它受到的安培力逐渐增大，静摩擦力也随之增大，当磁感应度增大到b所受安培力F与最大静摩擦力f相等时开始滑动.
感应电动势：E=

(3分)

棒b将要运动时，有f=B_tIL ∴B_t=

根据B_t=B₀+

,得t=1.8s
回路中产生焦耳热为Q=I²2rt=0.036J
(2)由图象可得到拉力F与t的大小随时间变化的函数表达式为 F=F₀+

当b棒匀加速运动时，根据牛顿第二定律有： F-f-F_安=ma
F_安=B_0-IL I=

v=at ∴F_安=

联立可解得F=f+ma+

(2分)

将据代入，可解得a=5m/s² f=0.2N

考点：
点评：本题是力学和电磁学的综合题，综合运用了电磁感应定律、能量守恒定律以及共点力平衡问题，

◎ 知识点

专家分析，试题“如图甲，在水平桌面上固定着两根相距0.2m,相互平行的无电阻轨道P和轨道一端固定一根电阻为0.0lΩ的导体棒a，轨道上横置一根质量为40g、电阻为0.0lΩ的金属棒b，两棒相距0.…”主要考查了你对【磁场对通电导线的作用：安培力、左手定则】等知识点的理解和应用能力。关于这些知识点的“档案”，你可以点击相应的链接进行查看和学习。