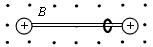如图所示,圆形匀强磁场半径R="l"cm,磁感应强度B=IT,方向垂直纸面向里,其上方有一对水平放置的平行金属板M、N,间距d=1cm,N板中央开有小孔S。小孔位于圆心O的正上方,
◎ 题目
如图所示,圆形匀强磁场半径R="l" cm,磁感应强度B=IT,方向垂直纸面向里,其上方有一对水平放置的平行金属板M、N,间距d=1cm,N板中央开有小孔S。小孔位于圆心O的正上方,S与0的连线交磁场边界于A.两金属板通过导线与匝数为100匝的矩形线圈相连(为表示线圈的绕向,图中只画了2匝),线圈内有垂直纸面向里且均匀增加的磁场,穿过线圈的磁通量变化率为△Φ/△t=100Wb/s。位于磁场边界上某点(图中未画出)的离子源P,在纸面内向磁场区域发射速度大小均为v=5  ×105m/s,方向各不相同的带正电离子,离子的比荷q/m=5×107C/kg,已知从磁场边界A点射出的离子恰好沿直线AS进入M、N间的电场.(不计离子重力;离子碰到极板将被吸附)求: ×105m/s,方向各不相同的带正电离子,离子的比荷q/m=5×107C/kg,已知从磁场边界A点射出的离子恰好沿直线AS进入M、N间的电场.(不计离子重力;离子碰到极板将被吸附)求: (1)M、N之间场强的大小和方向; (2)离子源P到A点的距离; (3)沿直线AS进入M、N间电场的离子在磁场中运动的总时间(计算时取π=3). |
◎ 答案
(1)E=U/d=106N/C,方向竖直向下(2)PA=r=  cm (3) t=2t1=2×10-8s cm (3) t=2t1=2×10-8s |
◎ 解析
:(1)由法拉第电磁感应定律得M、N之间的电压U=n△Φ/△t=100×100V=102V。 M、N之间场强的大小E=U/d=106N/C,方向竖直向下。 (2)离子在匀强磁场中做匀速圆周运动,由qvB=mv2/r, 解得r=  cm。 cm。如图所示,tanθ=R/r,解得θ=30°。 由图中几何关系可知离子源P到A点的距离PA=r=  cm。 cm。(3)离子在匀强磁场中做匀速圆周运动的周期T=2πm/qB。 离子第一次在磁场中运动的时间t1=T/6=πm/3qB=2×10-8s。  离子进入电场后做匀减速直线运动,在电场中运动距离x=v2/2a.,a=qE/m, 解得x=0.75cm<d。 因此离子不会打在M板上,会以相同的速率从A点反向再进入磁场。由对称性,离子在磁场中运动的总时间t=2t1=2×10-8s。 点评:此题考查法拉第电磁感应定律、带电粒子在电场中匀变速直线运动、在匀强磁场中匀速圆周运动等知识点。 |
◎ 知识点
专家分析,试题“如图所示,圆形匀强磁场半径R="l"cm,磁感应强度B=IT,方向垂直纸面向里,其上方有一对水平放置的平行金属板M、N,间距d=1cm,N板中央开有小孔S。小孔位于圆心O的正上方,…”主要考查了你对 【磁场对运动电荷的作用:洛伦兹力、左手定则】 等知识点的理解和应用能力。关于这些知识点的“档案”,你可以点击相应的链接进行查看和学习。- 最新内容
- 相关内容
- 网友推荐
- 图文推荐
上一篇:(18分)如图所示,光滑的绝缘平台水平固定,在平台右下方有相互平行的两条边界MN与PQ,其竖直距离为h=1.7m,两边界间存在匀强电场和磁感应强度为B=0.9T且方向垂直纸面向外的
下一篇:试判断下列各图中带电粒子受洛仑兹力方向或所带电荷种类或运动方向。
零零教育社区:论坛热帖子
| [家长教育] 妇产科专家告诉你:到底多大年龄,才算高龄产妇?不妨提前了解下 (2023-03-11) |
| [高考] 2022 西安电子科技大学《软件工程》大作业答案 (2022-04-25) |
| [家长教育] 孩子为什么会和父母感情疏离? (2019-07-14) |
| [教师分享] 给远方姐姐的一封信 (2018-11-07) |
| [教师分享] 伸缩门 (2018-11-07) |
| [教师分享] 回家乡 (2018-11-07) |
| [教师分享] 是风味也是人间 (2018-11-07) |
| [教师分享] 一句格言的启示 (2018-11-07) |
| [教师分享] 无规矩不成方圆 (2018-11-07) |
| [教师分享] 第十届全国教育名家论坛有感(二) (2018-11-07) |

![在阴极射线管上方平行放置一根通有强电流的长直导线,其电流方向从右向左,如图,阴极射线将[]A.向纸内偏转B.向纸外偏转C.向上偏转D.向下偏转](http://www.00-edu.com/d/file/2023-04-06/afc15db5ef0b908ef1f22f71501be2b5.gif)
![从阴极射线管发射出一束电子,在磁场的作用下发生偏转。下列各图对磁场与电子偏转情况所作的描述正确的是[]A、B、C、D、](http://www.00-edu.com/d/file/2023-04-06/9805e916bf7180b462f2e91d06890878.gif)