未来人类要通过可控热核反应取得能源,要持续发生热核反应,必须把温度高达几百万摄氏度以上的核材料约束在一定的空间内.约束的办法有多种,其中技术上相对较成熟的是用磁场
◎ 题目
| 未来人类要通过可控热核反应取得能源,要持续发生热核反应,必须把温度高达几百万摄氏度以上的核材料约束在一定的空间内.约束的办法有多种,其中技术上相对较成熟的是用磁场约束核材料,称为“托卡马克”装置.如图所示为这种装置的简化模型:有环形边界的匀强磁场(b区域)围着磁感应强度为零的圆形a区域,a区域内的离子向各个方向运动,离子的速度只要不超过某值,就不能穿过环形磁场的外边界而逃逸,从而被约束. 设环形磁场的内半径R1=0.50m,外半径R2=1.0m,若磁场的磁感应强度B=1.0T,被约束的离子比荷
(1)完成核反应方程:
(2)若a区域中沿半径0M方向射入磁场的离子不能穿出磁场的外边界,粒子的速度不能超过多大? (3)若要使从a区域沿任何方向射入磁场的速率为2×107m/s的离子都不能越出磁场的外边界,则b区域磁场的磁感应强度B至少要有多大?  |
◎ 答案
 (1)核反应方程中,质量数守恒,核电荷数守恒,所以有:
(2)速度越大,轨迹圆半径越大,要使沿0M方向运动的离子不能穿越磁场,则其在环形磁场内的运动轨迹圆中最大者与磁场外边界圆相切 设轨迹圆的半径为r1,则:
代入数据解得 r1=0.375m 设沿该圆运动的离子速度为v1,qv1B=
即 v1=
代入数据得v1=1.5×107m/s (3)设离子以v2的速度沿与内边界圆相切的方向射入磁场且轨道与磁场外圆相切时,则以该速度沿各个方向射入磁场区的离子都不能穿出磁场边界 (也可用图形表达 1分) 设轨迹圆的半径为r2,则r2=
设磁场的磁感强度为B1,由 B1=
代入数据得 B′=2.0T 答:(1) |

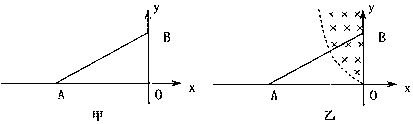
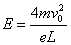

![静止在匀强磁场中的某放射性元素的原子核,当它放出一个α粒子后,其速度方向与磁场方向垂直,测得α粒子和反冲核轨道半径之比为44:1,如图所示,则[]A.α粒子与反冲粒子的动量](http://www.00-edu.com/d/file/2023-04-06/037384b85e1cb2b7f46c9d3cbe68861b.gif)
