如图所示,把中心带有小孔的平行放置的两个圆形金属板M和N,连接在电压恒为U的直流电源上.一个质量为m,电荷量为q的微观正粒子,以近似于静止的状态,从M板中心的小孔进入电
◎ 题目
| 如图所示,把中心带有小孔的平行放置的两个圆形金属板M和 N,连接在电压恒为U的直流电源上.一个质量为m,电荷量为q的微观正粒子,以近似于静止的状态,从M板中心的小孔进入电场,然后又从N板中心的小孔穿出,再进入磁感应强度为B的足够宽广的匀强磁场做中运动. 那么: (1)该粒子从N板中心的小孔穿出时的速度有多大? (2)该粒子在磁场中受到的洛仑兹力是多大? (3)若圆形板N的半径为R,如果该粒子返回后能够直接打在圆形板N的右侧表面上,那么该磁场的磁感应强度B至少为多大?  |
◎ 答案
(1)粒子进入电场的过程,根据动能定理有:qU=
所以粒子穿出小孔时的速度大小为: v=
(2)粒子在磁场中受到的洛仑兹力大小:f=qvB=qB
(3)粒子进入磁场做匀速圆周运动,洛伦兹力提供向心力:qvB=m
解得r=
所以粒子的圆轨道半径:r=
那么,粒子打在N板上的条件是:R≥2r=2
所以,粒子能够要在N板上,要求B至少为: B=2
|

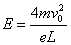

![静止在匀强磁场中的某放射性元素的原子核,当它放出一个α粒子后,其速度方向与磁场方向垂直,测得α粒子和反冲核轨道半径之比为44:1,如图所示,则[]A.α粒子与反冲粒子的动量](http://www.00-edu.com/d/file/2023-04-06/037384b85e1cb2b7f46c9d3cbe68861b.gif)
