婵ê鐡ㄥΣ鎼佹儑閸忕厧鐨炬俊顖d悍缁辨繄浠︽潏銊π﹂柣顏勵槸閸㈡煡鎳曞銉㈠亾閸屾侗鍎橀梻鍌ゅ枦椤㈡垶绂嶉崫鍕闂侇叏缍€缁旂喖鏁嶉悢鐑樼畳闁活亣鍋愬▔鈺呮儎閸繍妲遍柕鍡楀€规晶鐘虫叏鐎n喒鍋撴担瑙勑氱憸鐗堝釜缁辨繈宕i崼銉㈠亾娴e憡鍋樼憸鐗堝笒楠炴捇濡撮崒婵嗩仧闁告帞澧楅惈娆撳础濡ゅ嫬鍨佸☉鎾筹攻濡差剟鏁嶇仦钘夌.濞戞挸娲ら幏浼村及閵夈倗绉堕柕鍡嫹
如图所示,在半径为a(大小未知)的圆柱空间中(图中圆为其横截面),固定放置一绝缘材料制成的边长为L的弹性等边三角形框架DEF,其中心O位于圆柱的轴线上.在三角形框架DEF与圆柱

◎ 题目
如图所示,在半径为a(大小未知)的圆柱空间中(图中圆为其横截面),固定放置一绝缘材料制成的边长为L的弹性等边三角形框架DEF,其中心O位于圆柱的轴线上.在三角形框架DEF与圆柱之间的空间中,充满磁感应强度大小为B的均匀磁场,其方向平行于圆柱轴线垂直纸面向里.在EF边上的中点S处有一发射带电粒子的粒子加速器,粒子发射的方向均在截面内且垂直于EF边并指向磁场区域.发射粒子的电量均为q(q>o),质量均为m,速度大小均为v=
(1)为使初速度为零的粒子速度增加到v=
(2)带电粒子在匀强磁场区域内做匀速圆周运动的半径;. (3)若满足:从S点发射出的粒子都能再次返回S点,则匀强磁场区域的横截面圆周半径a至少为多大; (4)若匀强磁场区域的横截面圆周半径a满足第(3)问的条件,则从S点发射出的某带电粒子从S点发射到第一次返回S点的时间是多少? 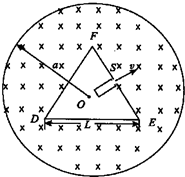 |
◎ 答案
(1)在粒子加速器中,带电粒子在电场中被加速,根据动能定理可知:qU=
U=
(2)带电粒子在匀强磁场中做匀速圆周运动,洛伦兹力提供向心力,由牛顿第二定律可知:qvB=m
解得r=
(3)设想某个带电粒子从S发射后又能回到S,则带电粒子的运动轨迹如图. 当带电粒子的运动轨迹同场区内切时,场区半径有最小值amin. amin=OG=OF+FG=r+
(4)带电粒子在磁场中做匀速圆周运动,由周期公式得:T=
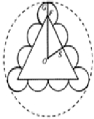 由轨迹图知,某带电粒子从S发射后第一次返回到S的时间为:t=
上一篇:如图所示,一个电子的质量为m,电荷量为e,让它以初速度v0,从屏S上的O点垂直于S射入其右边区域.该区域有垂直于纸面向里、磁感应强度为B的匀强磁场,该区域为真空.(1)求电子
下一篇:空间存在方向垂直于纸面向里的匀强磁场,图中的正方形为其边界.一细束由两种粒子组成的粒子流沿垂直于磁场的方向从O点入射.这两种粒子带同种电荷,它们的电荷量、质量均不同
零零教育社区:论坛热帖子
|

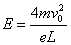

![静止在匀强磁场中的某放射性元素的原子核,当它放出一个α粒子后,其速度方向与磁场方向垂直,测得α粒子和反冲核轨道半径之比为44:1,如图所示,则[]A.α粒子与反冲粒子的动量](http://www.00-edu.com/d/file/2023-04-06/037384b85e1cb2b7f46c9d3cbe68861b.gif)

