(1)根据牛顿第二定律,由洛伦兹力提供向心力,则有:qvB=mv2r得r=mvqB(2)根据左手定则,依据几何特性,作图,则有该区域的面积:S=12πr2+14π(2r)2代入数据可解得:S=32π(mvBq)2
◎ 题目
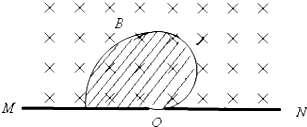 (1)根据牛顿第二定律,由洛伦兹力提供向心力, 则有:qvB=
得r=
(2)根据左手定则,依据几何特性,作图, 则有该区域的面积:S=
代入数据可解得:S=
答:(1)带电粒子进入磁场做圆周运动的半径得r=
(2)用圆规和直尺在图中画出带电粒子可能经过的区域(用斜线表示)并求出该区域的面积S=
|
◎ 答案

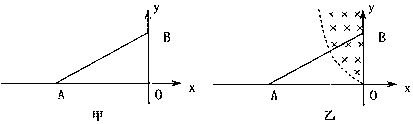

![静止在匀强磁场中的某放射性元素的原子核,当它放出一个α粒子后,其速度方向与磁场方向垂直,测得α粒子和反冲核轨道半径之比为44:1,如图所示,则[]A.α粒子与反冲粒子的动量](http://www.00-edu.com/d/file/2023-04-06/037384b85e1cb2b7f46c9d3cbe68861b.gif)
