如图所示，在直角坐标系的第Ⅰ象限0≤x≤4区域内，分布着强场E=28×106N/C的匀强电场，方向竖直向上；第Ⅱ象限中的两个直角三角形区域内，分布着磁感受应强度均为B=5.0×10-2T的匀
◎ 题目
如图所示，在直角坐标系的第Ⅰ象限0≤x≤4区域内，分布着强场E=
（1）求带电粒子在磁场中的运动半径； （2）求粒子在两个磁场及电场区域偏转所用的总时间； （3）在图中画出粒子从直线x=-4到x=4之间的运动轨迹，并求出轨迹与y轴和直线x=4交点的纵坐标．  |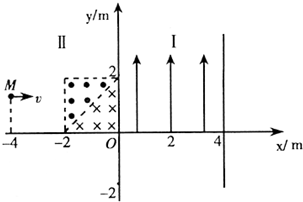
◎ 答案
◎ 题目
如图所示，在直角坐标系的第Ⅰ象限0≤x≤4区域内，分布着强场E=
（1）求带电粒子在磁场中的运动半径； （2）求粒子在两个磁场及电场区域偏转所用的总时间； （3）在图中画出粒子从直线x=-4到x=4之间的运动轨迹，并求出轨迹与y轴和直线x=4交点的纵坐标． |
◎ 答案
![静止在匀强磁场中的某放射性元素的原子核，当它放出一个α粒子后，其速度方向与磁场方向垂直，测得α粒子和反冲核轨道半径之比为44:1，如图所示，则[]A．α粒子与反冲粒子的动量](http://www.00-edu.com/d/file/2023-04-06/037384b85e1cb2b7f46c9d3cbe68861b.gif)
