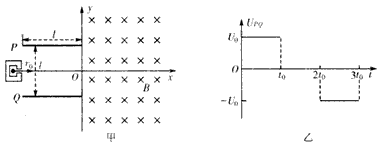
如图所示,两平行金属板A、B长度l=0.8m,间距d=0.6m.直流电源E能提供的最大电压为9×105V,位于极板左侧中央的粒子源可以沿水平方向向右连续发射比荷为q/m=l×107C/kg、重力
◎ 题目
如图所示,两平行金属板A、B长度l=0.8m,间距d=0.6m.直流电源E能提供的最大电压为9×105V,位于极板左侧中央的粒子源可以沿水平方向向右连续发射比荷为q/m=l×107C/kg、重力不计的带电粒子,射人板间的粒子速度均为v0=4×106m/s.在极板右侧有一个垂直纸面向里的匀强磁场,磁感应强度B=lT,分布在环带区域中,该环带的内外圆的圆心与两板间的中心重合于O点,环带的内圆半径Rl=
(1)问从板间右侧射出的粒子速度的最大值vm是多少? (2)若粒子射出电场时,速度的反向延长线与v0所在直线交 于O′点,试用偏转运动相关量证明O′点与极板右端边缘的水平距离x=
(3)为使粒子不从磁场右侧穿出,求环带磁场的最小宽度d.  |
◎ 答案
(1)由动能定理研究粒子从进极板到处极板的过程:
解出vm=5×106m/s  (2)证明:如图,设粒子在电场中的侧移为y,则
根据类平抛运动的规律研究粒子在水平方向和竖直方向的运动, 列出运动学等式: l=v0t y=
联立解得x=
(3)设环带外圆半径为R2, 所求d=R2-R1 粒子进入磁场后做匀速圆周运动,粒子刚好不出磁场的临界轨迹如图, 根据几何关系得: R12+rm2=(R2-rm)2  根据洛伦兹力提供向心力得: qvmB=m
联立解得:d=(2-
答:(1)从板间右侧射出的粒子速度的最大值是5×106m/s (2)证明如上. (3)环带磁场的最小宽度是0.586m. |
◎ 解析
“略”◎ 知识点
专家分析,试题“如图所示,两平行金属板A、B长度l=0.8m,间距d=0.6m.直流电源E能提供的最大电压为9×105V,位于极板左侧中央的粒子源可以沿水平方向向右连续发射比荷为q/m=l×107C/kg、重力…”主要考查了你对 【动能定理】,【带电粒子在电场中运动的综合应用】,【带电粒子在匀强磁场中的运动】 等知识点的理解和应用能力。关于这些知识点的“档案”,你可以点击相应的链接进行查看和学习。- 最新内容
- 相关内容
- 网友推荐
- 图文推荐
上一篇:如图所示,两足够长的平行光滑的金属导轨MN、PQ相距为L=1m,导轨平面与水平面夹角α=0°,导轨电阻不计.磁感应强度为B1=2T的匀强磁场垂直导轨平面向上,长为L=1m的金属棒ab垂直
下一篇:如图所示,匀强磁场的磁感应强度为B,方向垂直纸面向里,MN为其左边界.磁场中有一半径为R、轴线与磁场平行的金属圆筒,圆筒的圆心O到MN的距离OO1=3R,O1O所在直线与圆筒右侧
零零教育社区:论坛热帖子
| [家长教育] 妇产科专家告诉你:到底多大年龄,才算高龄产妇?不妨提前了解下 (2023-03-11) |
| [高考] 2022 西安电子科技大学《软件工程》大作业答案 (2022-04-25) |
| [家长教育] 孩子为什么会和父母感情疏离? (2019-07-14) |
| [教师分享] 给远方姐姐的一封信 (2018-11-07) |
| [教师分享] 伸缩门 (2018-11-07) |
| [教师分享] 回家乡 (2018-11-07) |
| [教师分享] 是风味也是人间 (2018-11-07) |
| [教师分享] 一句格言的启示 (2018-11-07) |
| [教师分享] 无规矩不成方圆 (2018-11-07) |
| [教师分享] 第十届全国教育名家论坛有感(二) (2018-11-07) |

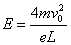

![静止在匀强磁场中的某放射性元素的原子核,当它放出一个α粒子后,其速度方向与磁场方向垂直,测得α粒子和反冲核轨道半径之比为44:1,如图所示,则[]A.α粒子与反冲粒子的动量](http://www.00-edu.com/d/file/2023-04-06/037384b85e1cb2b7f46c9d3cbe68861b.gif)
