如图(甲)为电视机中显像管的原理示意图,电子枪中的灯丝加热阴极而逸出电子,这些电子再经加速电场加速后,从O点进入由磁偏转线圈产生的偏转磁场中,经过偏转磁场后打到荧光
◎ 题目
如图(甲)为电视机中显像管的原理示意图,电子枪中的灯丝加热阴极而逸出电子,这些电子再经加速电场加速后,从O点进入由磁偏转线圈产生的偏转磁场中,经过偏转磁场后打到荧光屏MN上,使荧光屏发出荧光形成图象,不计逸出电子的初速度和重力.已知电子的质量为m、电荷量为e,加速电场的电压为U0,假设偏转线圈产生的磁场分布在边长为L的正方形区域abcd内,磁场方向垂直纸面,且磁感应强度随时间的变化规律如图(乙)所示.在每个周期内磁感应强度都是从-B0均匀变化到B0.磁场区域的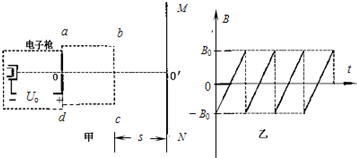 左边界的中点与O点重合,ab边与OO′平行,右边界bc与荧光屏之间的距离为s.由于磁场区域较小,电子速度很大,通过磁场时间t远小于磁场变化周期T,不计电子之间的相互作用. (1)若电视机工作中由于故障而导致偏转线圈中电流突然消失(其它部分工作正常),在荧光屏中心形成亮斑.设所有电子垂直打在荧光屏上之后,全部被荧光屏吸收,且电子流形成的电流为I,求荧光屏所受平均作用力F大小;(用I、U、e、m表示) (2)为使所有的电子都能从磁场的bc边射出,求偏转线圈产生磁场的磁感应强度的最大值B0; (3)荧光屏上亮线的最大长度是多少.(假设电子不会打在荧光屏之外) |
◎ 答案
 (1)由动能定理得:eU=
设时间t内有N个电子打在荧光屏上,则有I=
根据动量定理知:Ft=Nmv-0 由上三式得:F=I
(2)当磁感应强度为B0或-B0时(垂直于纸面向外为正方向),电子刚好从b点或c点射出,设此时圆周的半径为R,如图所示. 根据几何关系有:R2=l2+(R-
解得:R=
电子在磁场中运动,洛仑兹力提供向心力, 因此有:evB0=m
解得:B0=
(3)设电子偏离原来方向的角度为α, 根据几何关系可知:tanα=
设电子打在荧光屏上离O′点的最大距离为d,则d=
由于偏转磁场的方向随时间变化,根据对称性可知,荧光屏上的亮线最大长度为:D=2d=l+ |

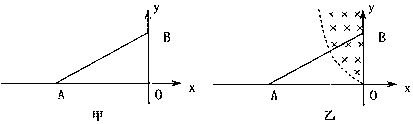
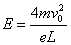

![静止在匀强磁场中的某放射性元素的原子核,当它放出一个α粒子后,其速度方向与磁场方向垂直,测得α粒子和反冲核轨道半径之比为44:1,如图所示,则[]A.α粒子与反冲粒子的动量](http://www.00-edu.com/d/file/2023-04-06/037384b85e1cb2b7f46c9d3cbe68861b.gif)
