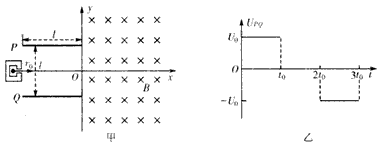
如图甲所示,两平行金厲板A,B的板长L=0.2m,板间距d=0.2m.两金属板间加如图乙所示的交变电压,并在两板间形成交变的匀强电场,忽略其边缘效应.在金属板上侧有方向垂直于纸
◎ 题目
如图甲所示,两平行金厲板A,B的板长L=0.2m,板间距d=0.2m.两金属板 间加如图乙所示的交变电压,并在两板间形成交变的匀强电场,忽略其边缘效应.在金 属板上侧有方向垂直于纸面向里的匀强磁场,其上下宽度D=0.4m,左右范围足够大,边界MN和PQ均与金属板垂直,匀强磁场的磁感应强度B=1x 1O-2T.在极板下侧中点O处有一粒子源,从t=0时起不断地沿着00'发射比荷
(1)求粒子进入磁场时的最大速率 (2)对于在磁场中飞行时间最长的粒子,求出其在磁场中飞行的时间以及由0点出发 的可能时刻. (3)对于所有能从MN边界飞出磁场的粒子,试求这些粒子在MN边界上出射区域的宽度.  |
◎ 答案
(1)设粒子恰从金属板边缘飞出时,AB两板间的电压为U0,由运动学公式及牛顿第二定律得:
qE1=ma1 E1=
t=
联立以上各式,解得,U0=400V<500V 设粒子进入磁场时的最大速率为vm,由动能定理得 q?
解得,vm=2
(2)分析可知,在磁场中飞行时间最长的粒子,其运动轨迹应在电场中向B板偏转,在磁场中恰好与上边界相切,如图所示,设粒子进入磁场时,速度v与OO′成θ角,在磁场中运动时间为  tm,由牛顿第二定律、平行四边形定则、几何关系及运动学公式得 qvB=m
v=
R(1+sinθ)=D T= |

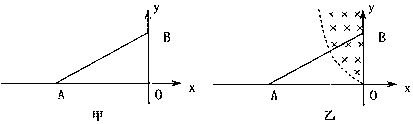
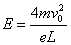

![静止在匀强磁场中的某放射性元素的原子核,当它放出一个α粒子后,其速度方向与磁场方向垂直,测得α粒子和反冲核轨道半径之比为44:1,如图所示,则[]A.α粒子与反冲粒子的动量](http://www.00-edu.com/d/file/2023-04-06/037384b85e1cb2b7f46c9d3cbe68861b.gif)
