如图所示,在x轴上方平面内存在方向垂直纸面向外的匀强磁场,磁感应强度大小为B.坐标原点O处有一离子源,可以在平行于纸面内向x轴上方(包括x轴)沿各个方向发射速率在0到υm之
◎ 题目
| 如图所示,在x轴上方平面内存在方向垂直纸面向外的匀强磁场,磁感应强度大小为B.坐标原点O处有一离子源,可以在平行于纸面内向x轴上方(包括x轴)沿各个方向发射速率在0到υm之间、质量为m、电量为q的负离子.不计离子的重力和离子之间的相互作用力,试分析: (1)若在t=0时刻发射的各种速率的离子仅沿+x方向,写出经过t=
(2)若在x轴的上方距离x轴d=
(3)若从t=0时刻开始向x轴上方各个方向发射各种速率的离子,求从t=0到t=
 |
◎ 答案
| (1)离子进入磁场中做圆周运动的半径为R,由牛顿第二定律得: qvB=m
解得最大半径Rm=
离子在磁场中运动的周期为T,则 T=
因为t=
y=x,且0≤x≤
(2)离子以最大速度υm向x轴正方向发射时,将到达屏的最右端. L1=
离子与屏刚好相切时,将到达屏的最左端. L2=
离子打在屏上的范围为-
|

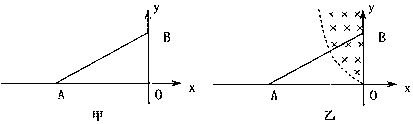

![静止在匀强磁场中的某放射性元素的原子核,当它放出一个α粒子后,其速度方向与磁场方向垂直,测得α粒子和反冲核轨道半径之比为44:1,如图所示,则[]A.α粒子与反冲粒子的动量](http://www.00-edu.com/d/file/2023-04-06/037384b85e1cb2b7f46c9d3cbe68861b.gif)
