如图所示,半圆有界匀强磁场的圆心O1在x轴上,OO1距离等于半圆磁场的半径,磁感应强度大小为B1.虚线MN平行x轴且与半圆相切于P点.在MN上方是正交的匀强电场和匀强磁场,电场场
| 1 |
| B1 |
(3)设粒子出B1磁场与半圆磁场边界交于Q点,如图所示,

找出轨迹圆心,可以看出四边形OO1O2Q四条边等长是平行四边形,所以半径O2Q与OO1平行.从Q点出磁场速度与O2Q垂直,所以垂直进入MN边界.
由几何关系:xQ=R-Rsinθ
粒子在电场中偏转,xQ=
| 1 |
| 2 |
| qE |
| m |
解上式得:y′′=
| mE |
| qB1B2 |
| mE | ||
q
|
|
答:(1)粒子初速度大小为,有界半圆磁场的半径为
| mE |
| qB1B2 |
(2)若撤去磁场B2,则经过P点射入电场的粒子从y轴出电场时的坐标为
| mE |
| qB2 |
|
| 1 |
| B1 |
(3)粒子打到y轴上的坐标与θ的关系式为y′′=
| mE |
| qB1B2 |
| mE | ||
q
|
|
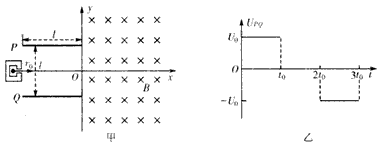
上一篇:如图所示,电子自静止开始经M、N板间的电场加速后从A点垂直于磁场边界射入宽度为d的匀强磁场中,两板间的电压为U,电子离开磁场时的位置P偏离入射方向的距离为L,在距离磁场
下一篇:如图所示,两平行金属板间距为d,电势差为U,板间电场可视为匀强电场;金属板下方有一磁感应强度为B的匀强磁场.带电量为+q、质量为m的粒子,由静止开始从正极板出发,经电场
零零教育社区:论坛热帖子
|

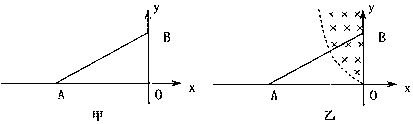

![静止在匀强磁场中的某放射性元素的原子核,当它放出一个α粒子后,其速度方向与磁场方向垂直,测得α粒子和反冲核轨道半径之比为44:1,如图所示,则[]A.α粒子与反冲粒子的动量](http://www.00-edu.com/d/file/2023-04-06/037384b85e1cb2b7f46c9d3cbe68861b.gif)
